ババ抜きの不平等さをベイズ統計で分析してみた
概要
年末に(もう5月ですが)芸能人がババ抜きをするテレビ番組を家族と観ているときにババ抜きが不平等なゲームであることに気が付きました。 定量的な評価を行うため、ちょうど勉強していたベイズ統計で検証しようと思いました。 以下が全体の流れです。
- ババ抜きの性質
- 仮説の提示
- 実験設定
- データ生成
- PyMC3による統計モデリング
- 結論
ちなみにこの記事に書いてあることは社内勉強会で発表したネタです。 ソースコードはGitHubに公開しています。 https://github.com/kbaigo/babanuki
ババ抜きの性質
仮説の説明に入る前に、ババ抜きについて整理しなければならないことがあります。
手札の偶奇
ババ抜きではjokerを入れたトランプ53枚を各プレイヤーに配ります。しかし、53は素数なのですべてのプレイヤーの手札の枚数が等しくなることはありません。例えば、3人だとそれぞれ18,18,17枚、4人だとそれぞれ14,13,13,13枚となります。
すると、カードが奇数の人や偶数の人が現れます。
これがこれから提示する仮説で重要になるため、プレイヤーの偶奇について詳しく知っておく必要があります。
そのために、まずはカードが変動する状況を考えます。カードが変動する状況は、
①同じナンバーのカードを2枚捨てる時
②カードを取る時
③カードを取られる時
です。
まず①同じナンバーのカードを2枚捨てる時ですが、この時はカードを2枚捨てているので捨てるプレイヤーの偶奇は変わりません。
次に②と③についてですが、基本的にこれはセットで行われるので1枚取って1枚取られれば手札の枚数は変わらず、偶奇は変わりません。
これだけ見ると手札の偶奇はゲームを通して変わらないように見えますが、実は二つ手札の偶奇が変わる場面があります。
1つ目は最初のプレイヤーがカードを引かれた時です。
ババ抜きは基本的に隣の人からカードを引いてからもう一方の隣の人にカードを引かれる動作を繰り返しますが、最初のプレイヤーは例外です。このプレイヤーだけは引かれてスタートし、偶奇が変わります。
2つ目はちょっと難しいですが、奇数プレイヤーがあがった後のプレイヤーがカードを引かれた時です。
自分の前のプレイヤー(自分が引く人)が残りカード1枚の状況を想像してみてください。その人はさらに前の人から1枚カードを取り、持っているカードが揃いました。彼は2枚のカードを捨て、あがります。するとあなたはカードを引くはずの人がいないため、カードを引くことなく自分のカードを隣の人に渡します。
仮説の提示
今回検証するババ抜きの不平等さを表す仮説は「ババ抜き手札が偶数だと有利説」です。
さて、ババ抜きは何人で対戦しても勝負の決着のパターンが二通りしかありません。勝負の決着に共通するのは「残りプレイヤー数が2人」で「片方があがる」という状況です。その中で、「片方があがる」パターンが二種類あります。
手札が偶数の人があがるパターン
簡単のため、上がるプレイヤーがjokerを持っていないとします。
偶数のプレイヤーがあがる時は、自分の持っているカードのうち、どちらかを引けば勝ちです。

一方で、手札が奇数のプレイヤーは自分の持っているカード1種類を引かなければ勝てません。

さて、実は偶数の人は奇数の人よりも「引いてあがりになるカード」の枚数が多いです。
奇数の人は8を引かないとあがれないのに対して偶数の人は8とAのどちらを引いてもあがれますね。最終形のこれだけ見れば、偶数の人が一手で上がる確率は2/3で、奇数の人は1/2です。
これと先ほどの手札の偶奇の変動が最初に引かれる人しか起こらないことを合わせて考えると、
自分が引かれてスタートするなら初期手札が奇数、それ以外なら初期手札が偶数
ならば有利な立場になれるということです。
ただ、このように最終形だけ見て有利不利を決定するのは早計の感もあります。また、先ほど述べたようにプレイヤーが上がることで残された人の偶奇が変わることがあるため、試合全体を通して初期手札が偶数のプレイヤーが奇数のプレイヤーに対してどの程度有利なのか定量的に述べることは困難です。
ですが、厳密解でなくともババ抜きの対戦をシミュレーションして統計的に推論することは可能です。
この記事の目標は、上記に上げた仮説について統計の立場から一つの見方を与えることです。
実験設定
仮説を検証するため、以下のように実験設定を行いました。
- カードをランダムに並べ替えた後、ランダムに選んでプレイヤーに分配する
- プレイヤーが他のプレイヤーからカードを取る際はランダムに選択する
- プレイヤー数は3人で固定(並び順も固定)
- 2パターンの並び方で5000戦ずつ対戦し両者のゲームを比較

左のパターンは「平等っぽい」ゲームで、右のパターンが「不平等っぽい」ゲームです。
左のゲームは最初に引かれるプレイヤーが奇数なので、ゲーム開始と同時にカードを一枚引かれて偶数の状態でカードを引く立場になります。残りの二人は言うまでもなく偶数の時にカードを引く立場になります。仮説を真とすれば、この3人には大して勝率に差は出なさそうです。(先に挙げた手前の奇数の人があがったときの問題がありますが、限られた状況でしか起きないためいったん置いておきます)
それに対して、右のゲームは初めの人が奇数で引く立場になります。さらに、3番目のプレイヤーも奇数で引く立場になります。つまり2番目のプレイヤーだけが有利(っぽそう)な立場にいます。
このように2パターンで分けて特に興味があるのは、「プレイヤーの並び順を変えただけで勝率に影響がでるか」というところです。
データ生成
上記の実験設定で合計10000回のシミュレーションを行います。
以下が、その結果を表す棒グラフです。

縦軸は敗北(最後の一人になった)数で、横軸はプレイヤーです。
赤線は33%を示す線で、平等なゲームであれば棒グラフの頂点はこのあたりに分布するはずです。
平等なゲームの結果
思惑通り、このゲームではプレイヤー全員の敗北数に差はなさそうです。
ただ、少し気になるのが若干勝率のよいplayer1と他の二人より負けているplayer2です。
この結果は、おそらく以下のように説明することができます。
- 3人でババ抜きをするとカードの分配は17枚,18枚,18枚となるため、player1だけカードの数が少ない。ババ抜きは手札が0枚になるとかつゲームなので、単純にplayer1は有利となる。
- 前述したように、player1があがるとplayer2の手札が奇数となる。仮説が正しければ、残されたplayer2はplayer3よりも勝ちづらくなる。
不平等なゲームの結果
このゲームは、実験設定によって仮説が正しいときにplayer2が勝ちやすいようにしました。
結果をみても明らかにplayer2が勝っています。
この結果から「手札の偶奇は勝率に影響する」と結論付けることもできますが、もっと知りたいのは何%程度勝率に影響するかどうかです。
1%であれば「そんな変わらないじゃん」という人もいると思いますが、10%変わればおそらく多くの人が「手札の偶奇は勝率に影響する」と感じるはずです。
このように結果を定量的に述べるため、統計的な解析方法の力を借ります。
PyMC3による統計モデリング
生成したデータを用いて、PyMC3による統計モデリングを行います。
実験データの単位は、以下のように1ゲームごとに生成され、自分が敗北したときは1、勝ったときは0となるようにしています。
| player1 | player2 | player3 | |
|---|---|---|---|
| ゲーム1 | 1 | 0 | 0 |
| ゲーム2 | 0 | 1 | 0 |
| ゲーム3 | 1 | 0 | 0 |
| ゲーム4 | 0 | 0 | 1 |
| ゲーム5 | 0 | 1 | 0 |
平等なゲーム
平等なゲームは仮説の正しさを前提に「平等」とされています。
ゆえに、平等なゲームを統計的に「平等」と言うことができれば、その結果はやはり仮説を支持します。
モデルは切片のみの一般化線形モデル(GLM)で、尤度関数はBernoulli分布、リンク関数はシグモイド関数を使用します。 また、MCMCサンプラーはNUTSです。
player1_worst = fair_game_result['p1_worst'].values player2_worst = fair_game_result['p2_worst'].values player3_worst = fair_game_result['p3_worst'].values with pm.Model() as model: theta1 = pm.Normal('theta1', mu=0, sd=100) theta2 = pm.Normal('theta2', mu=0, sd=100) theta3 = pm.Normal('theta3', mu=0, sd=100) p1 = pm.Deterministic('player1', pm.math.sigmoid(theta1)) p2 = pm.Deterministic('player2', pm.math.sigmoid(theta2)) p3 = pm.Deterministic('player3', pm.math.sigmoid(theta3)) diff_p1_p2 = pm.Deterministic('diff_player1_player2', p1 - p2) diff_p1_p3 = pm.Deterministic('diff_player1_player3', p1 - p3) y1 = pm.Bernoulli('y1', p = p1, observed=player1_worst) y2 = pm.Bernoulli('y2', p = p2, observed=player2_worst) y3 = pm.Bernoulli('y3', p = p3, observed=player3_worst) with model: trace = pm.sample(1500, random_seed=21)[500:] pm.plot_posterior(trace, varnames=['player1','player2','player3'], round_to=3, credible_interval=0.95, kind='hist', ref_val=0.33333) pm.plot_posterior(trace, varnames=['diff_player1_player2', 'diff_player1_player3'], round_to=3, credible_interval=0.95, kind='hist', ref_val=0) pm.summary(trace)
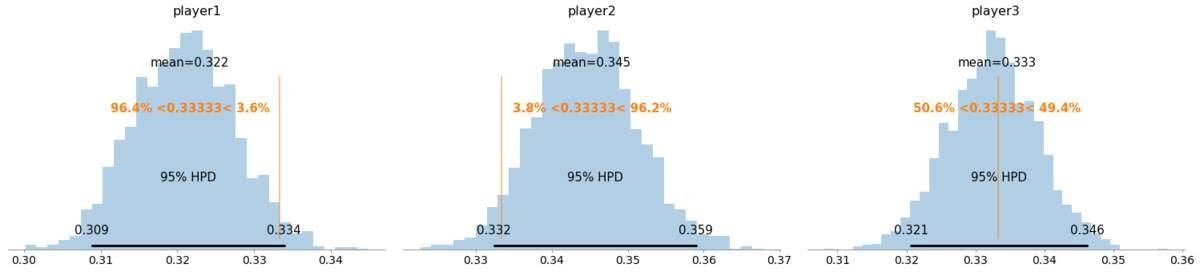
横軸が各プレイヤーの勝率(Bernoulli分布のp)を示していて、縦に引かれているオレンジ色の線が33.33%の線です。
黒い横線は95%確信区間(credible interval)で、「このプレイヤーの勝率は95%の確率でこの区間の中に入る」と主張することができます。
player3は綺麗に勝率が33.33%を平均とするように分布していますが、やはりplayer1とplayer2の結果には偏りがあるように見えます。
33.33%線が95%確信区間の中にいればこのゲームは「95%の確率で平等」とも言えますが、先ほど述べたplayer1の手札少ない問題などがあるため、もう少し注意深く分析してみます。

これは「player1とplayer2の勝率」および「player1とplayer3の勝率」を単純に引き算した分布です。真に平等なゲーム(勝率が33.33...%)であれば、それは0のまわりに分布するはずです。
player1とplayer2では95%確信区間は平均0を含まず、2%程度差をつけています。また、player3との差も、1%程度の差をつけています。
これを素直に受け取れば、手札の少ないプレイヤーは3人対戦のときで1,2%程度有利になると主張することができます。 手札の枚数が重要に見えるババ抜きにおいて、初期手札の枚数が1%,2%程度しか勝率に影響しないという結果は少し意外なのではないでしょうか。
不平等なゲーム
データを見ても不平等なゲームでplayer2が有利なのは明らかなので、ここでは不平等なゲームのplayer2と平等なゲームのplayer2でどの程度勝率に差が出るかを見ていきたいと思います。
ここで、もう一度実験設定を見てみましょう。

今注目しているのは右下の「手札が偶数のplayer2」なので、ここで発生した勝率の差は「自分の手札、引く順番が同じでも他のプレイヤーの偶奇が違うだけで何%勝率が変わってしまうか」ということになります。
基本的にモデリングは平等なゲームの時と同じですが、今回は変数項も加えたGLMで、不平等なゲームの場合のみ生起する項theta2があります。
p2_unfair = unfair_game_result['p2_worst'].values p2_fair = fair_game_result['p2_worst'].values with pm.Model() as model: theta1 = pm.Normal('theta1', mu=0, sd=100) theta2 = pm.Normal('theta2', mu=0, sd=100) unfair_p = pm.Deterministic('unfair_probability', pm.math.sigmoid(theta1 + theta2)) fair_p = pm.Deterministic('fair_probability', pm.math.sigmoid(theta1)) diff_p = pm.Deterministic('diff_probability', fair_p - unfair_p) y1 = pm.Bernoulli('y1', p = unfair_p, observed=p2_unfair) y2 = pm.Bernoulli('y2', p = fair_p, observed=p2_fair) with model: trace = pm.sample(1500, random_seed=21)[500:] pm.plot_posterior(trace, varnames=['unfair_probability', 'fair_probability'], round_to=3, credible_interval=0.95, kind='hist', ref_val=0.33333) pm.plot_posterior(trace, varnames=['diff_probability'], round_to=3, credible_interval=0.95, kind='hist', ref_val=0) pm.summary(trace)

一見してわかるように、不平等なゲームでのplayer2の勝率は33.33%からかけ離れています。
この結果は、このMCMCサンプリングの範囲では100%平等ではないと主張できます。
次に、両者の差を取った勝率の分布を見てみましょう。

この結果から、席順が異なるだけで95%の確信をもって10%前後勝率に差が生じる主張できます。
これは仮説を支持するのに十分な結果といえるのではないでしょうか。
結論
統計モデリングの結果から、ババ抜きでは初期手札が偶数であるか、奇数であるかが勝率にかなりの影響を及ぼすということがわかりました。また、単純な初期手札の枚数もわずかながら影響を与えるようですが、偶奇に比べると微々たるものであることもわかりました。
これまでの結論を踏まえると、ババ抜きをするときは「自分を起点にするときは初期手札の枚数が奇数」、「それ以外の場合は初期手札が偶数であれば有利となる」と言え、そのうえで「初期手札が少なく」、「自分の前の人の初期手札が偶数だと望ましい」ということになります。
それでは、自分が有利になるような場面を考えてみましょう。責任はもたないので悪用はしないでください。
また、対戦人数によって手札が偶数のプレイヤーと奇数のプレイヤーの数は異なるため、自分が一番有利かどうかはきちんとその場で考える必要があります。
自分がカードを配るディーラーだとして、そのうえでカードを配る前に始点の人と周り順を決めたとしましょう。
もし自分が始点だった場合は自分の手札が奇数になるようにカードを配ります。
初期手札の偶奇をコントロールする方法は簡単で、プレイヤーの人数と配り始めの人、配る順の方向が決まればそれぞれのプレイヤーのカードの枚数はただ一つに定まります。あとは自分の手札が奇数になるよう計算して配り始めの人と配る方向を決めるだけです。
自分が始点以外の場合は同様のことを自分が偶数になるようにすればよいだけです。
こんな素振りをしている人を見つけたら不平等なゲームを仕掛けようとしている可能性があるので覚えておけば自衛に使えるかもしれませんね。
逆にフェアなゲームがしたい方はこういうことはしないようにしましょう。