近況63．人生のビバーク

あれよあれよという間に３月も最終日です。

気温の変化の大きさに身体がついていけないようで、調子が今一つよくありません。悪いというほどでもないので、日常の生活に大きな支障はないのですが、集中力に欠ける感じで記事の更新が滞っています。

少なくとも日に２回は食事を摂れているし、眠れない日が続いている訳でもないし、大きな不安で息苦しかったり、体が震えたりということもないし、その内、何とか好転するだろうと気楽にいたのですが、まだ低空飛行が続いています。

啓蟄に合わせた前回の記事に

下書きは増えたものの、どれも記事にできないまま…

と書きましたが、その状況は変わらず。「もう、いいやあ」とあきらめてしまう前に、せめて今月中にもう一記事と、一月に２記事は最少更新数ながら、何とか重い腰を上げているところ。とはいえ、この記事を投稿したら、また腰を下ろして、また一眠りとなるかも知れません。まぁ、私の人生にも、もっと大変だった時期はあったので、こんな不調、大したことないという気分です。

どこで知ったのか忘れましたが、記事代わりに、ある話を紹介します。

雪山登山に挑戦していたチームが猛吹雪で進退敵わず、岩陰にテントを張ってビバーク（予定通りに下山できず、山中で緊急に夜を明かすこと）することになりました。

チームには若手とベテランがいて、一つのテントで過ごします。テントは強風にあおられ、何度も飛ばされそうになり、その度、若手が不安を口にします。でも、ベテランは「なかなかの猛吹雪だな。人生で5番目位か。これをやり過ごしたら、お前たちも一人前と言えるかも知れないな。」と余裕たっぷりです。

しかし、ついにテントは飛ばされてしまいました。若手は、もう駄目だと絶望しますが、ベテランは動じません。

「テントが飛ばされたらお終いというなら、俺はもう３回は人生をやり直したぞ。岩陰があるだけ今回はマシだ。救助要請もしてあるのだから弱気になるな。朝には助けが来る。」

チーム全員、布にくるまり身を寄せ合って凌ぎます。

そして、穏やかでよく晴れた朝を迎えました。

ビバークして迎えた朝

救助隊に発見された時、若手は皆大喜びでした。

救助隊のリーダーはベテランと知りあいでした。ベテランは礼を言います。

「ありがとう。希望が持てるなら嘘でもつき通せ。君の言葉が救いだった。あんな猛吹雪は初めてだったよ。」

「経験は積んだ量より、活かした回数さ。生還、おめでとう。」

きっと、実話ではないだろうなと思っています。

でもいいのです。大事なのは、実話かどうかではないと思うので。

ということで、このスランプは人生何度目かのビバークかも知れないと考えることにしました。吹雪が止めば、記事を書くでしょう。明日止むのか、まだ先かは不明ですけど。

tn103．啓蟄に出てくるもの

ついこの前、恵方巻を記事にしたつもりでいたら、もう啓蟄です。

下書きは増えたものの、どれも記事にできないまま28日になります。さすがに何とかしないと更新放置新記録になるので、啓蟄に合わせて書くと決めました。更新のない間、世に隠れて暮らしていたわけでもないですが、長い間を空けて記事更新をするのにいいタイミングに思われます。下書き止まりの記事　の中には、機を逃しても完成させたいものもあるので、こそっと更新するかも知れません。

啓蟄は、冬の間、地中に閉じこもっている虫が動き始める頃とされます。「啓」には、開くや教える等の意味があります。「蟄」には、家にこもってじっと隠れているとの意味があり、冬ごもりをする虫の意味にも使われます。

啓蟄　イメージ

「啓蟄」との呼び名を知ったのは多分、浪人時代です。受験を終えた頃に知り、ああやっと表の世界に出られるんだとの感慨を持って受け止めた記憶があるので、大学合格がわかった1985年3月16日より後でしょう。

ちなみに、大学の合格通知はもらっていないと思い込んでいた記事はこちら。

母の家計簿を見るまで、間違った記憶のままでした。

どこから何が出てくるかわからないものです。

いえ、どこで何を忘れてしまうかわからないもの、と言うべきでしょうか。

啓蟄に　もぐらたたきを　思い出し

なお、二十四節気で啓蟄の次は春分。詳しくはこちら。

授業36．2024年度共通テストを少しやってみた（３）数Ⅰ編

2024年度共通テストの平均点が報道されました。それで思い出しました。

ああ、数Ⅰ編をまだアップしてなかったな。

放置しても誰からもお咎めは無いだろうけれど、毎年少しだけでも解いてきた自分に申し訳ない気がするので、遅ればせながらアップします。

解いたのは数Ⅰの第１問のみ。小問として、［１］不等式（回答欄ア～サ）と、［２］集合（同シ～ノ）があり、配点は20点です。

第１問［１］不等式

ア部分

第１問　ア部分

nは整数です。√13は、√9＜√13＜√16なので、3＜√13＜4です。

ここで問題になるのは、√13が3.5以上かどうかです。それによって

6＜2√13＜7 （n=6）なのか、7＜2√13＜8 （n=7）なのかが変わります。

そこで3.5を2乗してみます。

    3.5
  X3.5
 ------
  17 5
105
------
12.25

このことから、√12.25=3.5 なので、√13 は3.5より大きいとわかります。

従って、n＝７

ア＝７

イウ部分

イウ部分

アは７より、a=2√13-7 となり

b=1/a

  =1/(2√13-7)

です。これを変形します。ルートが含まれている分母の整数化には(a-b)(a+b)=a^2-b^2が使えるので、

b/(2√13+7)=1/(2√13-7)(2√13+7)
b/(2√13+7)=1/(2√13)^2-49
b/(2√13+7)=1/4X13-49
b/(2√13+7)=1/52-49
b/(2√13+7)=1/3
b=(7+2√13)/3

となり、

イ＝７、ウ＝3

エオカ部分

エオカ部分

a^2-9b^2＝（2√13-7）^2-9((7+2√13)/3)^2 で計算できますが、

ここは、a^2-9b^2=(a+3b)(a-3b)を利用したいです、

a=2√13-7 なのに対して、先のイ、ウで、b=(7+2√13)/3と答えさせたのは、気づきにくくする意図があったのでしょうか。aの無理数と実数の並びに合わせて、b=(2√13+7)/3とします。

そうすると、3b=7+2√13 なので、(a+3b)(a-3b)にそれぞれ代入すると、

a^2-9b^2=(2√13-7+7+2√13)(2√13-7-7-2√13)

a^2-9b^2=(4√13)×(-14）

a^2-9b^2=-56√13

となり、

エ＝-　オ＝5　カ＝6

キク部分

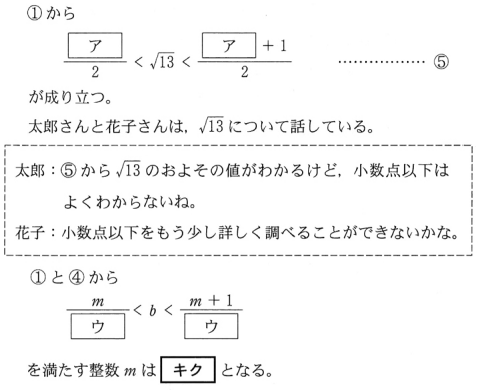
キク部分

ここで、①を変形した式が登場。⑤は、7/2<a<8/2 と同じ。

ウ=３、b=(2√13+7)/3 でした。

ここでは、m/3< (2√13+7)/3 < (m+1)/3 で整数 m を問うているわけです。

これは、m< (2√13+7) < (m+1) と同じ。 

①の式で、7＜2√13＜8 と分かっているので、

7+7＜2√13+7＜8+7 となり、　

14/3<b<15/3 です。

m=14

キ=1、ク=4

ケ、コ、サ部分

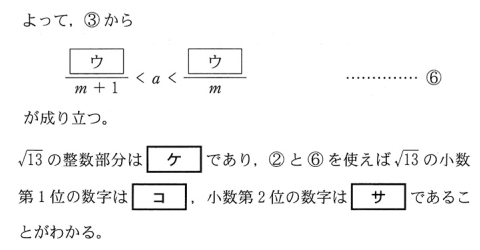
ケコサ部分

要するに、√13 を小数の近似値にして、小数第2位までの数字を出す問題です。

ここで、アを回答する方法が、本筋と違っていたのだろうなと思いました。でも、すでに3.5の2乗が12.25であると分かっています。36の2乗は1225+35+36で1296となり、3.6×3.6=12.96 です。恐らく、√13を小数の近似値にした場合、整数は３です。小数第1位は6でしょうし、小数第2位はおそらく０でしょう。それでも、念のため3.61の2乗を計算。

3.61×3.61=13.0321

13を超えてしまいました。これで確定です。小数にすると、3.60…となります。

ケ=3　コ=6　サ=0

本当は、⑥の式を変形して答える問題でしょうけど、もう、これでいいです。

第１問［２］集合

シスセ部分

シスセ部分

全体集合Uは［２，３，４，５，６，７，８，９］で要素は８個です。

a=4 だと、Aは［４，８］、b=5だとBは［５］。

数字の並びに注意して

A∪B=［４，５，８］（AとBを合わせた部分）

シ＝４、ス＝５，セ＝８

ソタチ部分

ソタチ部分

a=2 だと、Aは［２，４，６，８］、

b=3 だとBは［３，６，９］B補集合は［２，４，５，７，８］です。

A∩B補集合［２，４，８］（AとB補集合が重なる部分）

ソ＝２、タ＝４、チ＝８

※ただし、回答欄にチ＝９としていて、痛恨の入力ミス。

ツテ部分

ツテ部分

a=2 だと、Aは［２，４，６，８］、b=3 だとBは［３，６，９］

A∪Bは［２，３，４、６，８，９］で、残りは５と７です

A∪B=C補集合∩D補集合で、５と７を含まないとなると

c＝５、d=７　であり、

ツ=５、テ＝７

トナニヌ部分

トナニヌ部分

A∪B∪C∪D＝［２，３，４，５，６，７，８，９］になるのは、先述のことを組み合わせて、a=2、b=3、c=5、d=7 となり、

ト＝２、ナ＝３、ニ＝５、ヌ＝７

ネノ部分

ネノ部分

この問題では、私が［2,6,8］⊂ A∪B∪C の「⊂」の意味を取り違えていたのが明らかになりました。「＝」と「⊂」の区別をしていなかったのです。

［2,6,8］⊂ A∪B∪C　を、AとBとCの要素を全て集めたものが［2,6,8］だと誤解したのです。＝と同じに考えました。

a=2だと［2,4,6,8］ですから、4を取り除く条件が必要として、必要条件だが十分条件ではないとして、ネ＝０としました。

b=6 だと［2,6,8］に必要なようですが、6は3の倍数でもあるため、必ず必要とはなりません。またb=6では［2,8］の条件を補えません。そのためノ＝４としました。

結果とおまけ

採点結果

答え合わせをした結果、入力ミスのチ（-2点）と問題文の勘違いネ（-1点）で誤答。

20点満点中17点でした。

でも、ノは問題を理解できていないのに、たまたま正解になったというだけです。

過去の共通テストの記事を振り返りました。

2023年度は数Ⅰ第１問に挑戦し、20点中20点でした。

2022年度は数Ⅰ第１問に挑戦し、30点満点中、16点でした。

2021年度は、数Ⅰで気になったところだけを解いて、採点はしていません。

点が取れると嬉しいというのはありますが、それ以上に問題を解けたことや、思い出せたこと、学習になったことの方が収穫という感じです。毎度の繰り返しになりますが、現役受験生だった頃の自分には、よくこうした問題を時間内に解けたなと感心してしまいます。

おまけ　集合の記号の打ち込み方

ところで、回答はするのには、Windowsの標準のソフト（アプリ）のメモ帳に記入する形です。こんな感じ。

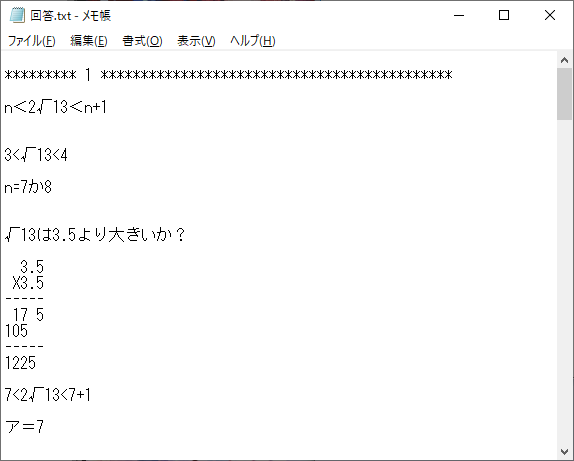
回答はメモ帳で作成

手書きにしない理由は、２つ。

１）パソコンを常用しているため筆記用具を出すのが面倒。加えて保存場所がはっきりしているので、探す手間もいらず、過去の問題とも比較できること。

２）特に数学の記号や打ち込み方の学習にもなる。

記号で言えば、√（るーと）、∪（カップ）、∩（キャップ）等があり、

2乗を表すのに^2と表記することなども検索して知りました。

今回の収穫は集合関連の記号の打ち込み方。

知っている方も多いと思いますが…

習合関連の記号の打ち込み方

「しゅうごう」と打ち込んで変換キーを複数回押した際に変換候補の一覧が出てきます。その縦に細長い一覧の右下隅に□に→のついたマークがあります。それをクリックすると、さらに集合に関する記号の一覧が出てくるので、必要なものをクリックするとOK。∩ や ∪ も選択できると知りました。今回、⊂はこの方法で打ち込みました。

タイトル画像