オイラー・マクローリンの総和公式について（１）

前々からゼータ関数 \zeta(s) の値を、どのように算出するのか知りたいと思っていました。とくに s<1 の値がどうして有限の値として得られるのか不思議に思っていました。ウェブを見るとゼータ関数の計算式が色々と見つかったのですが、なぜそのような式が成り立つのか、今ひとつ分かりません。ただ、計算法の元祖はグラームの用いた「オイラー・マクローリンの公式 (略して以後、ＥＭ公式と呼ぶ)」であることを知りました。ゼータ関数の計算法は後々述べることにし、まず「ＥＭ公式」を導いてみます。ＥＭ公式の導出については色々と紹介されているのですが、その導出過程や図式的意味が省略されているように見受けられましたので、ここではその辺を多少くどいくらいに記載したいと思います。
図１は y=f(x) を積分区間 k～(k+1) で積分する様子を示しますが、ＥＭ公式は、積分面積と、それを台形近似した面積の差を表す式としてとらえることができます (ここで k は整数)。

f:id:wabin379:20191219175258p:plain
図１．積分区間 (k)～(k+1)
ＥＭ公式の導出にあたっての主要な関係式は、部分積分の公式、すなわち「(u\cdot v)'=u'v+u\cdot v' \ 」から得られる
[u(x)\cdot v(x)]=\int u'(x)\cdot v(x)\,dx+\int u(x)\cdot v'(x)\,dx \tag{1} です。
上式(1)において u=(x-k-1/2),\ v=f(x) とおくと「\int u'v\,dx - [u\cdot v] = -\int u\cdot v'dx」なので、部分積分の関係式
\begin{align*} \int_{k}^{k+1} & 1 \times f(x)dx - [(x-k-1/2)\cdot f(x)]_{k}^{k+1} \\ &= -\int_{k}^{k+1}(x-k-1/2)\cdot f'(x)dx \tag{-} \end{align*}すなわち
\begin{align*} \int_{k}^{k+1}f(x)\,dx - \{f(k+1)+f(k)\}/2 \\= -\int_{k}^{k+1}(x-k-1/2)\cdot f'(x)\,dx \tag{2} \end{align*}が成り立つ。
これを図１と対比すると、式(2)の左辺は「曲線 [y=f(x)] の下の面積」から「台形の面積 ABFC」を引いた「弓形の面積 CFf」になる。
また f'(x)\:dx=df(x)\equiv df であることに注意し、式(2)の右辺を変形すると \{\int (1/2)df-\int(x-k)df\} = \{[f(x)/2]_{k}^{k+1} - \int(x-k)df\} となり、これは
\{f(k+1)-f(k)\}/2 - \int_{k}^{k+1} (x-k)\:df(x) \tag{3}となる。式(3)の第１項は「三角形 CFE の面積」であり、第２項は「面積 CfFE」に相当する。よって、式(2)の右辺は、左辺同様「弓形の面積 CFf」を表している。このことは、部分積分公式から導かれた式(2)の図式的説明になっています。

つぎに式(2)の両辺を k=M,M+1,M+2,\dots,N-1 について加えてみます。すると、式(2)の左辺第２項は
\begin{align*} \hspace{5mm} \frac{1}{2} &\sum_{k=M}^{N-1} \{f(k)+f(k+1)\} \\ &=\frac{1}{2} \{f(M)+f(M+1)+f(M+1)+f(M+2) \\ &\hspace{6mm} + \ \dots\ +f(N-2)+f(N-1)+f(N-1)+f(N)\} \\ &=\{\sum_{k=M+1}^{N-1}f(k)+\frac{1}{2}f(M)+\frac{1}{2}f(N)\} \\ &\hspace{6mm} +\frac{1}{2}\{f(M)+f(N)-f(M)-f(N)\ =\ 0 \} \\ &=\sum_{k=M}^{N} f(k) - \frac{1}{2} \{f(M)+f(N)\} \end{align*}
となるので、式(2)は
\begin{align*} \int_{M}^{N}f(x)\,&dx - \sum_{k=M}^{N}f(k) + \{f(M)+f(N)\}/2 \\ &= -\int_{M}^{N}(\{x\}-1/2)\,f'(x)\,dx \tag{4} \end{align*}となる。
ここで \{x\}\equiv (x\ mod\ 1) であり、図１における (x-k) に相当する。

式(4)より、総和を定積分で計算することのできる式(5)が得られる。
\begin{align*} \sum_{k=M}^{N}f(k) &= \int_{M}^{N}f(x)\,dx + \{f(M)+f(N)\}/2 \\ &+ \int_{M}^{N}(\{x\}-1/2)\,f'(x)\,dx \tag{5} \end{align*}
式(5)の右辺第３項は、ベルヌーイ多項式 \{B_1(t)\equiv (t-1/2),\ t=0\sim1\} を用いると
\int_{M}^{N}(\{x\}-1/2)\,f'(x)\,dx = \int_{M}^{N} B_1(\{x\})\,f^{(1)}(x)\,dx \tag{6} と表すことができる。ここで、ベルヌーイ多項式の性質、 \{B'_m(t)=m\ B_{m-1}(t)\ , \hspace{2mm} (m \geq 1 )\}　から導かれる
\begin{align*} &u'\equiv \{B_i(t) = B'_{i+1}(t)/(i+1)\} \\ &u\ \equiv \{\int B_i(t)\,dt = \frac {1}{(i+1)} \int B'_{i+1}(t)\,dt = \frac {1}{(i+1)} B_{i+1}(t)\} \tag{7} \end{align*} 　および、 v=f^{(i)}(x) を、部分積分の公式(1)「\int u'v\,dx = [u\cdot v] - \int u\cdot v'dx」に代入すると
\begin{align*} \frac{1}{i\ !} \int_M^N B_i (\{x\}) f^{(i)}(x)\,dx &= \frac{1}{(i+1)!}B_{i+1}\{f^{(i)}(N) - f^{(i)}(M) \} \\ & - \frac{1}{(i+1)!} \int_M^N B_{i+1}(\{x\}) f^{(i+1)}(x)\,dx \tag{8} \end{align*} が得られる。この式ではベルヌーイ多項式 B_i(t) と、ベルヌーイ数 B_i の関係
B_i(\{M\})=B_i=B_i(\{N\})\tag{9} を用いている。
式(8)を、式(6)に逐次的に適用すると
\begin{align*} \int_{M}^{N}&(\{x\}-1/2)\,f'(x)\,dx = \int_{M}^{N} B_1(\{x\})\,f^{(1)}(x)\,dx \\ = &+ \frac{1}{2\ !}B_{2}\{f^{(1)}(N) - f^{(1)}(M) \} \\ &- \frac{1}{2\ !} \int_M^N B_{2}(\{x\}) f^{(2)}(x)\,dx \\ %=& \frac{1}{i\ !} \int_M^N B_i (\{x\}) f^{(i)}(x)\,dx \\ = &+ \frac{1}{2\ !}B_{2}\{f^{(1)}(N) - f^{(1)}(M) \} -\frac{1}{3\ !}B_{3}\{f^{(2)}(N) - f^{(2)}(M) \} \\ &+ \frac{1}{3\ !} \int_M^N B_{3}(\{x\}) f^{(3)}(x)\,dx = \ \dots \ \\ = & \sum_ {i=2}^{L} \frac{(-1)^i}{i\ !} B_i \{f^{(i-1)}(N)-f^{(i-1)}(M)\} \\ &+ \frac{(-1)^{L+1}}{L\ !} \int_M^N B_{L}(\{x\}) f^{(L)}(x)\,dx \tag{10} \end{align*}
これを式(5)の右辺２項に代入すれば、以下に示す「オイラー・マクローリンの公式 (ＥＭ公式)」が得られる。
\begin{align*} \sum_{k=M}^{N}f(k) &= \int_{M}^{N}f(x)\,dx + \{f(M)+f(N)\}/2 \\ &+\sum_ {i=2}^{L} \frac{(-1)^i}{i\ !} B_i \cdot \big[f^{(i-1)}(x)\big]_M^N \ +\ R_L \tag{11} \end{align*}
ここで、R_L は剰余項(誤差項)であり
\begin{align*} R_L = \frac{(-1)^{L+1}}{L\ !} \int_M^N B_{L}(\{x\}) f^{(L)}(x)\,dx \tag{12}\end{align*} である。
この公式(11)の使用例として、「\sum_{k=1}^N k^2」 を求めてみると、下記の手書きメモに示すように、よく知られた「\sum_{k=1}^N k^2=N\,(N+1)\,(2N+1)\,/\,6」 を得ることができます。

f:id:wabin379:20191219175853j:plain
図２． \sum_{k=1}^N k^2 を算出する
上に示した使用例は Ｎ が有限の級数でしたが、ＥＭ公式は無限級数で本領を発揮します。この公式は s>1 とした場合のゼータ関数 \zeta(s)=\sum_{k=1}^{\infty}1/k^s の値はもちろんのこと、s<1 のときにも有限値を算出し,\zeta(-1)=-1/12 となります。なぜ、そのような有限値がえられるのかは、のちほど別の記事で述べることにします。さらには、s が複素数でも対応できます。

[参考文献] …
UBASICによる解析入門、森本 光生 (著)、日本評論社 (1992/12)

流行りの「Python」に pygame を導入してみた。

８年ぶりに「月刊誌：日経ソフトウェア」を買いました。８年前頃に流行っていたプログラミング言語は「Java」などでしたが、今回購入した2019年11月号を見ると、今や「Python」が花ざかりですね。ついつい、日経ソフトのムック本の「いろいろ作りながら学ぶ！Python入門」も購入してしまいました。

そのムック本の第1章に「Pythonista 3」の「scene モジュール」を使ったアニメーションが紹介されていましたが、それらは「iPhoneやiPadのようなiOSデバイス」向けの「App Store」からのみインストール・利用可能とのことでした。

そこで「scene モジュール」のかわりに、Windowsでアニメーションできる「pygame という モジュール」を使ってみることにしました。

私は「Anaconda 環境」で「Python」を導入しているので、モジュールのインストールは「pip コマンド」ではなく「conda コマンド」で行うよう心がけていました。

そこで、まず「Anaconda プロンプト」にて「conda install pygame」なるコマンドを実行してみましたが、モジュールが見つからないというエラーが出てしまいました。そこで、つぎに「conda install -c cogsci pygame」としてみましたが、またもやエラーが出て、インストールできませんでした。

そこで、ついにしびれを切らし「Anacondaの環境下では、pip を使うな」という禁じ手にさからい「pip install pygame」コマンドを実行したところ、幸い、無事に「pygame」をインストールできました。
そして pygame のフォルダ「%CONDA_PREFIX%\Lib\site-packages\pygame」が
作成されました。

私の場合は幸いＯＫとなりましたが、必ずしもＯＫとなる保証はないので、Anaconda自体を再インストールする覚悟を持って pip を 使用してください。

なお、ついでながら、Anacondaを再インストールする場合、その前にアンインストールせねばなりませんが、Windowsの場合、コントロールパネルの「プログラムと 機能」にてアンインストールすることになります。私は、今まで2回ほどAnacondaを再インストールしたことがあります。

pygameの例題のひとつは「python -m pygame.examples.aliens」なるコマンドで実行できます。これはインベーダーゲームであり、矢印キーで左右移動、空白キーで相手を攻撃できます。

「Yahoo!ブログ」から「はてなブログ」へ移行

2019年12月に「Yahoo!ブログ」のサービスが終了することに伴い、2019年9月10日に「はてなブログ」へ移行いたしました。前々から「はてなブログ」には「数式」や「プログラムコード」を記述できる機能があるとのことを伝え聞いてましたので、そのような機能を欲していた私としては、いつかは「はてなブログ」を利用したいと思っていました。

「はてなブログ」には色々な編集モードがありますが、初心者の私としては、まずは「はてな記法モード」を使うことにしました。

例えば「はてな記法モードのTeX記法」で「数式」を [tex:e^{i\pi} + 1 = 0] と書くと、期待どうり「e^{i\pi} + 1 = 0 」と表示されました。

また「プログラムコード (言語名=python)」を 「>|python|」と 「 ||<」で挟むと、以下のように表示されました。

L1=[0,1,2];  L1.insert(0, 100);   # [100, 0,1,2]
L1.insert(-1, 200);  L1           # [100, 0,1, 200, 2]
L1.insert( 0, [-1,-2,-3]);  L1    # [[-1,-2,-3], 100, 0,1, 200, 2]

接続不能となった無線LANの復旧の顛末の一例

ＩＴ #その他インターネット
接続不能となった無線LANの復旧の顛末の一例

　2015年5月19日、突然、パソコン(ＰＣ)からルータの無線LANにつながらなくなり、スマホからもつながらなくなりました。使っているルータはNTTのPR-S300SEです。以前にもこのようなことがありＰＣを再起動したらつながったので、今回もＰＣを再起動してみましたがダメでした。メールのやりとりを行う必要があったので、ＰＣをルータの有線LANの方ににつなぎかえ、当座をしのいでいました。

　5月24日、メールのやりとりが一段落したので、ＰＣから有線LANケーブルをはずし、無線LANへの接続モードに移行しました。しかし依然ＰＣからの無線LANへのアクセスはできません。スマホには、以前接続していたネットワーク名(SSID)は表示されるのですが、圏外と表示されてしまいます。

　5月25日、イライラして、ルータの無線LANカードを抜き差ししてみましたが、やはり接続できません。ここで頭を冷やし、ルータの取扱説明書を読み返してみると、無線LANカードを抜き差しする際に、ルータの電源プラグを抜くようにと書かれていました。

　そこで、ルータ(PR-S300SE)の電源を抜き、有線LANケーブルも抜き、無線LANカードを抜き差しし、10秒以上待ってから電源を入れると、無線LANに接続できるようになりました。

　結局、私の場合、この操作によってルータが再起動し、無線LAN接続が復旧したものと思います。この方法はＷＥＢであまり紹介されていませんでしたので、復旧方法の一例としてこのブログで紹介することといたします。この方法は単なる一例で、必ずしも安全かつ有効であるとは断言できませんので、復旧は自己責任で行ってください。

GeoGebra による 幾何図形の描画

ＩＴ #ソフトウェア
GeoGebra による 幾何図形の描画
 
マウス操作などで幾何図形を作図したり、数式や解をグラフ表示することができる"GeoGebra"というソフトウェアを導入してみました。"GeoGebra"はアニメーション的描画もできますので、動的数学ソフトウェアとも呼ばれています。
 
当初は"Google"の"Chromeウェブストア"から "ChromeアプリとしてのGeoGebra"を導入しました。しかしヘルプに書かれている事と操作メニューの内容が異なっており、作画ファイルの保存やエクスポートが困難(できない？)となってしまいました。そこで、ＰＣのディスクの容量は136MBほど消費しますが、この"GeoGebraのインストール"のサイトからWindows版をダウンロードしインストールしました。
 
"GeoGebra"は"オプション／言語"で日本語で表示することもできますし、"日本語ヘルプ"や"GeoGebra日本"のサイトを参考にすることもできますので、わりと容易に幾何図形を描くことができるようになりますが、実際に作図してみないと操作方法を良くのみこめないので、このブログに示すような図を作成してみました。
 
この図はユークリッドにイメージ 1よるピタゴラスの定理の証明を示す図であり、正方形ACFGの面積は長方形CJKEに等しくなることを示しています。
この図に手を加えて、同等な面積が {正方形ACFG}/2＝{ΔACF} から {ΔBCF} ⇒ {ΔACE} ⇒ {ΔCEJ}＝{長方CJKE}/2  へと遷移する様子をアニメーション表示できるようにしました。
 
そして、操作メニューの"ファイル／共有"をクリックして、このアニメーション図を"GeoGebraTube"に投稿(アップロード)してみました。興味のある方は投稿先のＷＥＢページを参照してみてください。
そのページの[生徒向けワークシート]をクリックすると、左側ペインに数式ビューが、右側ペインにグラフィックスビューが表示されます。そのグラフィックスビューの左下に表示されたプレイボタンを押すと、同等な面積が {ΔACF} から {ΔCEJ} へと移行していきます。
 
(追記-1) ここでは正方形ACFGの面積は長方形CJKEに等しくなることのみを示しましたが、同様な手順によって、正方形BAHIの面積が長方形BDKJに等しくなることも示すことができます。

W32Tex や Asymptote の導入(インストール)に成功するまで経緯（１）

ＩＴ #ソフトウェア
W32Tex や Asymptote の導入(インストール)に成功するまで経緯（１）
 
最近 {Asymptoteのつかいかた} というサイトで "Asymptote" という面白そうなソフト(プログラム言語)が存在することを知りました。このソフトを使うと様々な図形をベクタグラフィックで描くことや、数式をTeX流に表示ができそうですので、早速インストールしてみました。
ところがテストしてみると「フォントが見つからない」とのエラーが出てしまい、作図できませんでした。本稿では、そのエラーを回避し、作図が可能となるまでの経緯を記述いたします。
 
【１】初期インストール／テスト
資料１={Asymptoteのつかいかた／インストール}を参考にして、Windows 8.1 のフォルダ"D:\dt13a" のもとに 、"W32TeX" と "Asymptote" などをインストールしました。フォルダ "\dt13a" 内には "W32TeX","Asymptote" のみでなく "gs", "Ghostgum" というフォルダも作られます。
資料１内の{ためしてみる}に記載されているとおりに
       size(4cm);
       filldraw(polygon(6), palegreen, deepgreen+2);
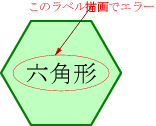
       label("{\huge 六角形}");
という内容のテキストファイル "hex.asy" を作り、コマンドプロンプトで「asy -f png hex.asy」を実行してみました。すんなり、六角形という文字ラベルの付いた六角形画像が描かれると思いきや、
       mktexmf: empty or non existent rootfile
       Cannot find cmr12.mf
というようなエラーが続々と出てしまい、画像が表示されませんでした。
ただし、上記の"hex.asy"の３行目を取り去るかコメント化すると、ラベル表示無しで六角形画像が描かれます。
イメージ 1
その他にも色々なチェックをしてみました。チェックの方法については【４】に記載しておきましたが、この段階では「必要なフォントが見つからない」というエラーが出てしまい、うまくいきませんでした。
明らかに文字フォントが十分にインストールされていないようなので、フォルダ "W32TeX" を丸ごと削除し、{W32TeX}に記載されている方法でインストールをやり直してみたり、ダウンロードサイトを変更してみる等の事を試みましたが、結果は同じでした。
 
【２】不足フォントの入手
コマンドプロンプトで「asy -f png hex.asy」を実行した際のエラーメッセージを参考にすると、不足しているフォントは cmr12.mf, cmr12.tfm, cmr12.pfb などであることがわかります。それらをキーワードにしてウェブを検索してみると、それらは「CTAN」の
  [A1] cmr12.mf は … {http://www.ctan.org/tex-archive/fonts/cm/mf}.
  [A2] cmr12.tfmは … {http://www.ctan.org/tex-archive/fonts/cm/tfm}.
  [A3} cmr12.pfbは … {http://www.ctan.org/tex-archive/fonts/cm/ps-type1/bakoma/pfb}
に入っていることがわかります。
これらのサイト内の "zipファイル"をダウンロードし解凍すれば、必要とする物を含むファイル群を入手することができます。ただし、今の段階では "W32TeX" 内のどこにこれらのファイルを入れれば良いかわからないので「中間貯蔵フォルダ」を作り、そこにファイルを一旦収めました。
 
その中間貯蔵フォルダから、Asymptoteのコマンド「asy -f png hex.asy」を実行するカレントフォルダ内に必要なファイル（cmr12.mf, cmr17.mf, greekl.mf, greeku.mf, roman.mf, romanl.mf, romanu.mf, cmr12.pfb,cmr17.pfb）をコピーし直接入れてしまえば「label("{\huge 六形}");」という文が実行できるようになりました。ただし、なぜか、図が左端に寄ってしまって、左側の一部が欠けて表示されてしまいます。この原因は未だ不明です。
 
【３】不足フォントを"w32tex\share\"内に追加
不足フォントを追加する場合、たくさんの配布ファイルが収められたフォルダ "w32tex\share\texmf-dist" の方にではなく、"w32tex\share\texmf-local" のほうに入れることにしました。
"texmf-local"以下のフォルダ名をどのように命名すべきかわかりませんでしたが、該当する拡張子(.mf, .tfm, .pfb)のファイルが "texmf-dist\fonts" 内のどんなフォルダに入っているか、「CTAN」のどんな構成のフォルダに入っているか、などを調査勘案しつつも、自己流かつ適当に、フォルダ名称と構成を下記のように定めました。
  [B1]  *.mf  の収納場所 … {texmf-local\fonts\source\public\cm\mf\}
  [B2]  *.tfm の収納場所 … {texmf-local\fonts\tfm\public\cm\tfm\}
  [B3]  *.pfb の収納場所 … {texmf-local\fonts\type1\public\cm\pfb\}
まず [B1] を作成し、そこに中間貯蔵フォルダから "*.mf" をコピーしました。そして、Asymptoteのコマンド「asy -f png hex.asy」を実行すると [B2] が自動的に作り出されました。この時点では [B3] は必要なかったが "hex.asy" 内の「label("{\huge 六角形}")」を「label("{\huge Hex}")」に変更すると "cmr12.pfb" などが見つからないというエラーが発生しました。よってその時点で[B3]を作成し、そこに中間貯蔵フォルダから "*.pfb" をコピーするとエラーが消えました。
 
【４】チェック
以上で、Asymptoteのコマンド「asy -f png hex.asy」が実行できるようになり、画像が表示されるようになりました。その他にも "W32TeX" に含まれる "dviout" や "TeXworks" を使ってみることができますので、参考となるサイトを記載しておきます。
[C1] {日本語TeX のインストールのチェック}により「簡単なTeXのファイルからdviファイルを作成し、
      それを "dviout" で表示できるかどうかテスト」できます。
[C2] {TeXworks/使い方} に記載された例文を "TeXworks" で表示してみることができます。
 
【５】最後の一言
以上ながながと経緯を記述しましたが、問題は「"w32tex" のフォントをどのように追加するのか」ということでした。この問題に対し、ウェブで色々と検索・調査してみたのですが、的を得た記事には出会えませんでした。
ここでは【３】で述べたように、フォントを追加するフォルダの構成と名称を、自己流かつ適当に定めましたが、本当にこれでいいのかとの思いがあります。このように定めても、フォント検索の効率に影響しないのかという疑問が残っています。

「Microsoft Mathematics」によって、簡便に「数式の計算機能」を試す。

ＩＴ #ソフトウェア
"Microsoft Mathematics"によって、簡便に「数式の計算機能」を試す。
 
前回の投稿で「Wordの数式計算機能」について記述しました。この機能を使う場合、計算対象とする数式を「数式の挿入ボタン」を押し「数式エディタ」で「数式エリア」に入力する必要があります。そしてその「数式エリア」にカーソルをおき「数学リボン内」の「計算」もしくは「グラフ」を押す必要があります。よって「数式の計算機能」でどんなことができるのか簡単に知ることが困難です。

もっと簡便に「数式の計算機能」を試すために「Microsoft Mathematics 4.0」を導入してみることがお勧めです。このソフトは Word などとは独立に動くスタンドアロンソフトです。このソフトの側から数式の雛形が提示されるので、計算機能やグラフ化機能を簡便に試すことができます。
ただし、どこまで高度な式が計算できるかまでは試していません。私はより高度な式を計算する場合「Maxima」などを使っています。