wetchのブログ

他人に見られることを想定していない書き散らかし独習ノート．物理学とかVBAとか．

同型定理のイラスト

物理学・数学

ランキング参加中
知識

参考文献


以下，G, G' は群，H は部分群，N は正規部分群，e は単位元を表す．

準同型定理

定理 写像 f: G\rightarrow G' を準同型写像とする．このとき写像
\bar{f} : G/\operatorname{Ker}f\rightarrow G' : a\operatorname{Ker}f \mapsto f(a)
はwell-defined（代表元 a の取り方によらず定義される）で，単射準同型写像となる．したがって値域の方を狭めて
\bar{f} : G/\operatorname{Ker}f \rightarrow \operatorname{Im}f : a\operatorname{Ker}f \mapsto f(a)
と再定義すればこれは同型写像．すなわち G/\operatorname{Ker}f \simeq\operatorname{Im}f.

これのイラスト化を考えてみたのだけど，rhidetoのblogに載ってる下の絵が一番分かりやすかった．


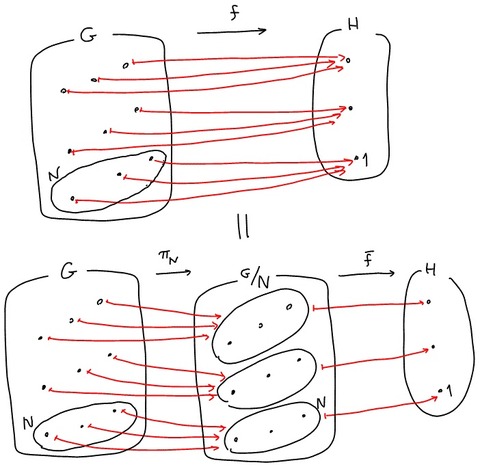
https://livedoor.blogimg.jp/rhideto/imgs/5/8/5809b1ce-s.jpg
rhidetoのblog : 例6. 剰余群と準同型定理

自分なりにも書いてみる．

まず G,G' とそれらをつなぐ写像 f がある．

G,G' とそれらをつなぐ写像 f がある

f は単射でないから f(k)=e' となる k\ne e もあり得るし，全射でないからどこからも矢印が飛んでこない c'\in G' も存在し得る．
全射じゃない部分は無視（\operatorname{Im}f \subset G' の部分だけを考慮）して，単射じゃない分は G の元を類別する（G/\operatorname{Ker}f を考える）ことで解消できる．

準同型定理のイラスト

そんなふうに \bar{f} を構成すると，この絵のように1対1対応がつけられる．

第1同型定理

準同型定理のことを第1同型定理と呼ぶことも多いようだけど，ここでは参考文献に倣ってそれとは異なる定理を挙げる．

定理 全射準同型写像 f:G\rightarrow G'， 正規部分群 N'\triangleleft G' とする．このとき N:=f^{-1}(N') \subset G は G の正規部分群であり，写像
g: G/N\rightarrow G'/N' : aN\mapsto f(a)N'
は同型写像となる．すなわち G/N \simeq G'/N'.

これは準同型定理において，G' の元を類別して（あるいは膨らませて）正規部分群による剰余群 G'/N' に置き換えるイメージ．
まず G,G',N' と f がこんな感じであって：

G,G',N'とf がこんな感じである

N' に対応する N:=f^{-1}(N') \subset G がこうなってて：

Nがこうなっている

G,G' を N,N' でそれぞれ割って G/N, G'/N' とすれば，この2つには1対1対応が付けられる．

第1同型定理のイラスト

第3同型定理

第1同型定理は群 G と別の群 G' のお話だったが，第2，第3同型定理では G' が出てこなくて，全部 G の中が舞台になっている．これはさっきまで G' として考えていたところを，同型性を利用して G の中に埋め込んでいる*1と考えることができる．

先に第3の方を説明しよう．第1同型定理を使うと第2より説明しやすい．

定理 N,M をともに G の正規部分群とし，N \subset M とする．このとき M/N は G/N の正規部分群であり，写像
f : G/N \rightarrow G/M : aN\mapsto aM
は全射準同型写像であって，写像
\bar{f}: G/M \rightarrow (G/N)\ /\ (M/N): aM \mapsto a(M/N)
は同型写像となる．すなわち G/M \simeq (G/N)\ /\ (G/M).

G/M, G/N, M/N を絵にしてとりあえず定理を絵にするとこんな感じか．

第3同型定理のイラスト

証明は準同型定理において \operatorname{Ker}f=M/N, \operatorname{Im}f=G/M とおくみたいな感じだが，第1同型定理からの導出のイメージとしては，まず第1同型定理の N を M に，N' を N に，G' を G/M に書き換えて，

N を M に，N' を N に，G' を G/M に書き換える．

で，G/M を G の中に埋め込むといった感じ．

G/M を G の中に埋め込む

第2同型定理

定理 部分群 H \subset G，正規部分群 N \subset G とする．このとき HN は G の部分群，H\cap N は H の正規部分群であり，写像
f : H/(H\cap N) \rightarrow HN/N : h(H\cap N) \mapsto hN
は同型写像となる．すなわち H/(H\cap N) \simeq HN/N.

イラスト化にあたっては HN と H\cap N をどう表すかというのが肝だろうと思う．検索すると下図のような感じの図がよくヒットする．


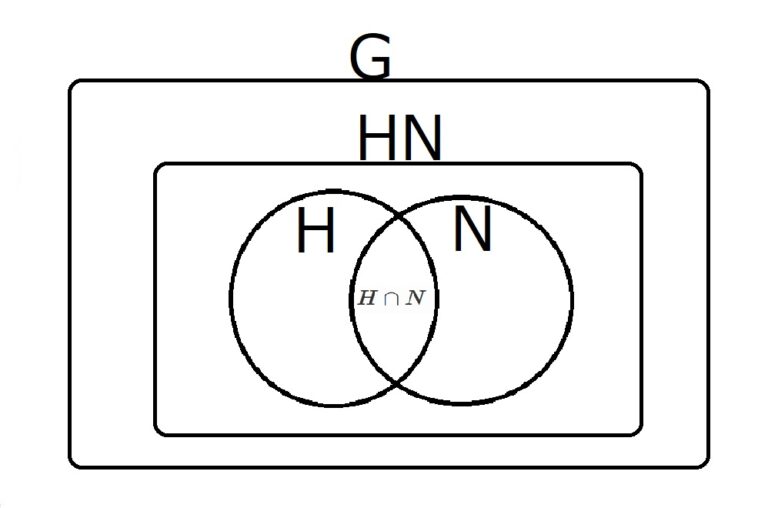
https://mathtano.com/wp-content/uploads/2023/08/isomorphism-theorems-2-768x508.jpg
第二同型定理を分かりやすく解説 | マスタノ！〜数学の楽しみ方〜

だが，乗積表のようなものを考えた方がより構造を表しうるんじゃないかと思う．

N と H の乗積表．注意：N\cap H は e 以外にもある．また，ある積 n_i h_j と別の積 n_i' h_j' はダブっていることもある．

で，この絵から H/(H\cap N), HN/N を考えると，

第2同型定理のイラスト

と，こんな感じになって同型になっていることが分かる．あとは第3同型定理のときと同様にして H を HN の中に埋め込む．

参考

群以前の定理

準同型定理の本質というか，代数構造を省いたら結局こういうことらしい．

定理 集合 X,Yに対し，写像 f:X\rightarrow Yを使ってX の同値関係 x\sim x' \Leftrightarrow f(x)=f(x') を定める．このとき X/\sim は完全代表系と同一視できる．すなわち写像
\phi: X/\sim \ \rightarrow \operatorname{Im}f: C(x)\mapsto f(x)
は全単射で，その逆写像は
\phi^{-1}: \operatorname{Im}f\rightarrow X/\sim \ : y\mapsto f^{-1}(\{y\}).
ここで C(x):=\{x'\in X|x'\sim x\} は x を代表元とする同値類．

*1:埋め込み（写像）とは，部分群 H \subset G から元の群 Gへの写像 \imath : H\rightarrow G : h\mapsto h のこと（明らかに単射準同型写像）．念のためメモしておいた．

摂動入門：2次方程式の級数根

物理学・数学

こんなことしてたって量子力学の理解にはなにひとつつながらないというのに．．．

参考文献

やりたいこと

やりたいことのイメージ
2次方程式（赤線）
ax^2+bx+c=0 \tag{1}
の根（赤丸）を求めたいが，根の公式を知らないとする．ただし1次方程式（青線）の根（青丸）は分かる：
bx+c=0 \Leftrightarrow x=-c/b.
a が微小なら，1次方程式の根から2次方程式の根へのずれも微小だろうと予想されるので，1次方程式の知識を使って近似でもいいので求めたい．そこで2次方程式の根は
\displaystyle x=-\frac{c}{b}+\sum_{i=1}^\infty \phi_i a^i \tag{2}
という a の級数と考えて，係数\phi_iをどうしたらいいか考えていく．
（図の左の方には2次方程式のもう一つの根が見切れているはずだが，今は無視する．）

考察

2次方程式(1)に級数式(2)を代入し，aのべきで整理してみると，

\begin{align} 0 =& \left(\frac{c^2}{b^2} + b\phi_1\right)a + \left(b\phi_2 - \frac{2c}{b}\phi_1\right)a^2 \\ &+ \sum_{i=3}^\infty\left(-\frac{2c}{b}\phi_{i-1} + b\phi_i + \sum_{j=1}^{i-2} \phi_{i-j-1} \phi_j\right) a^i.\end{align} \tag{3}
となる．
∵とにかく代入する．
\begin{align}0 &= a\left(-\frac{c}{b}+\sum_{i=1}^\infty \phi_i a^i\right)^2+b\left(-\frac{c}{b}+\sum_{i=1}^\infty \phi_i a^i\right)+c \\ &= a\left(\frac{c^2}{b^2}-\frac{2c}{b}\sum_{i=1}^\infty \phi_i a^i + \sum_{i=1}^\infty\sum_{j=1}^\infty \phi_i \phi_j a^{i+j}\right) + b\sum_{i=1}^\infty \phi_i a^i.\end{align}

2重和の項についてはk=i+j+1と変数変換して
\displaystyle = \frac{c^2}{b^2}a - \frac{2c}{b}\sum_{i=1}^\infty \phi_i a^{i+1} + \sum_{k=3}^\infty\sum_{j=1}^{k-2} \phi_{k-j-1} \phi_j a^k + b\sum_{i=1}^\infty \phi_i a^i.

第3項のkをiに書き戻す．第2項のi+1を改めてiと書く．
\displaystyle = \frac{c^2}{b^2}a - \frac{2c}{b}\sum_{i=2}^\infty \phi_{i-1} a^i + \sum_{i=3}^\infty\sum_{j=1}^{i-2} \phi_{i-j-1} \phi_j a^i + b\sum_{i=1}^\infty \phi_i a^i.

i=1,2を級数の外に出し，\sum_{i=3}^\infty(\cdots)a^iでまとめると式(3)になる．■

aがどんな値でも式(3)が成り立つためには，各係数が 0 であることが必要だから，ここから\phi_iが求まる：
\displaystyle \left\{ \begin{align} \phi_1 &= -\frac{c^2}{b^3}, \\ \phi_2 &= \frac{2c}{b^2}\phi_1 = -\frac{2c^3}{b^5}, \\ \phi_i &= \frac{2c}{b^2}\phi_{i-1} -\frac{1}{b} \sum_{j=1}^{i-2} \phi_{i-j-1} \phi_j, \quad (i=3,4,\dots).\end{align}\right. \tag{4}

係数の付き方が複雑だが，実は等比数列的な構造があり，

\displaystyle \psi_i:=\frac{2b}{c}\left(\frac{b^2}{2c}\right)^i \phi_i,\quad (i=1,2,...)
と変数変換すると
\displaystyle \left\{ \begin{align} \psi_1 &= -1, \\ \psi_2 &= -1, \\ \psi_i &= \psi_{i-1} -\frac{1}{4} \sum_{j=1}^{i-2} \psi_{i-j-1} \psi_j, \quad (i=3,4,...) \end{align}\right. \tag{5}
と簡潔に書ける．その代わり級数根(2)は
\displaystyle x=-\frac{c}{b}+\frac{c}{2b}\sum_{i=1}^\infty \psi_i \left(\frac{2ac}{b^2}\right)^i \tag{6}
となる．

力尽きた

とは言っても漸化式(4)や(5)の一般項は出せないし，式(2), (6)に代入したら本当に

\displaystyle x=\frac{-b+\sqrt{b^2-4ac}}{2a}
をaで展開したものになるのかも分からん．

c数とかq数とか，他

物理学・数学

参考文献

量子力学で c数とかq数っていうのを聞くが，これって他にも種類があったんだ．．．というのを文献で知ったのでメモを置いておく．
まあ他の種類がどのくらい広く使われてるのかは知らんけど．

できるだけ本に書いてある通りに書き写してみる．

以上2つはディラックによる命名．

  • e数：exterior algebra（外積代数）に属する数．すなわち体 K:=\mathbb{R}\text{ or }\mathbb{C} として， N次元ベクトル空間 K_N 上の完全反対称R重線形形式の集合 \Lambda^Rの直積集合
    \mathfrak{G}(K_N^*):=\Lambda^1\times\cdots\times\Lambda^N
    に外積\wedgeを定義して，そのK_N^*上の外積代数\mathfrak{G}(K_N^*)の元がe数（K_N^* は K_N の双対空間）．
  • a数：anticommuting number. 反可換数であるグラスマン数の略記．任意のe数を
    \mathsf{a}=(\lambda_0,\lambda_1,...,\lambda_N) \in\mathfrak{G}(K_N^*),\quad\lambda_n\in\Lambda^n
    と表現した時に，\lambda_1以外はすべて0であるようなe数の集合
    \Gamma_N:=\{\mathsf{a}|\mathsf{a}=(0_0,\lambda_1,0_2,...,0_N)\} \subset\mathfrak{G}(K_N^*),\quad\lambda_1\in K_N^*
    （0_nは\Lambda^nのゼロ元）の元がa数．

性質

  • 2個のa数の積 \xi_1\xi_2 は任意のe数と可換．しかし \xi_1\xi_2=0 でない限り \xi_1\xi_2 はc数ではない．「2個」の部分は「一般に偶数個の」としてよい．
  • 任意のa数の積 \xi_1\xi_2\dots\xi_R においてm番目とn番目の因子を入れ替えれば符号が変わる．つまり，任意のa数の積 \xi_1\xi_2\dots\xi_R は添え字(1,2,...,R)に関して完全反対称．


本の続きに，a数を使った（古典）解析力学や量子力学についての説明があるが，今のところ全然読み進められない．．．

（計算メモ）反対称行列の固有値と固有ベクトル

物理学・数学

折角計算したので，捨て置くのも勿体ないし書き残しておく．

問題

3次の反対称行列

\begin{bmatrix}0 & c & -b \\ -c & 0 & a \\ b & -a & 0\end{bmatrix}

の固有値と固有ベクトルを求めよ．

結果

r^2:=a^2+b^2+c^2とする．

1個目の固有値\lambda・固有ベクトル\boldsymbol{v}は

\lambda=0, \quad \boldsymbol{v} = \begin{bmatrix}a\\b\\c\end{bmatrix}

2個目は

\lambda=ir,\quad \boldsymbol{v} = \begin{bmatrix}ab+irc\\b^2-r^2\\bc-ira\end{bmatrix}

3個目は

\lambda=-ir,\quad \boldsymbol{v} = \begin{bmatrix}ab-irc\\b^2-r^2\\bc+ira\end{bmatrix}

2, 3個目の固有ベクトルを求めるのが大変だったけど，一度見つけてしまえば検算は簡単．なので証明は省略．

todo: 反対称行列を4次に拡張し，また計量もミンコフスキー計量とするとどうなる？

マクスウェル応力テンソルの固有値・固有ベクトル

電磁気学

対称行列を見ると対角化したくなる病気．

参考文献

やりたいこと

電磁場のイラストレートを企てているが，クーロン力やローレンツ力がうまく書けない．
これらに関係するマクスウェル応力テンソルが対称行列なので微分形式で書けるものでないからというのもあるし．
その辺，よく考えようとしたところ，そもそもマクスウェル応力の構造をよく理解してないことに気付いた．
とりあえず対称行列の構造は対角化して主方向を調べたら分かりそうなんだが，文献とかググったりして調べてもよく分からないので計算してみた．

前提条件と表記上の注意

  • 計算を簡略化するために真空中とし，物理次元を適当に規格化して\epsilon_0=\mu_0=1, \boldsymbol{D}=\boldsymbol{E}, \boldsymbol{B}=\boldsymbol{H}であるかのように扱う．
  • ベクトル\boldsymbol Eに対して，そのノルムの表記をE^2=|\boldsymbol{E}|^2=\boldsymbol{E}\cdot\boldsymbol{E}=E_kE_kのようにいろいろ，気分で使い分けている．
  • 計量テンソルの符号は\eta_{\mu\nu}=(-1,+1,+1,+1).
  • 物理量の次元を\sim[\text{SI単位}]で表す．たとえばT\sim[\mathrm{J/m^3}].

3次元

問題の定式化

任意に電場\boldsymbol{E}=E_i=(E_1,E_2,E_3)，磁場\boldsymbol{H}=H_i=(H_1,H_2,H_3) \sim[\mathrm{N^{1/2}/m}]が与えられたとき，マクスウェル応力

\begin{align} T&= \boldsymbol{E}\otimes\boldsymbol{E} + \boldsymbol{H}\otimes\boldsymbol{H} -\mathrm{I}\, \frac{1}{2}(E^2+H^2)\\ &=\begin{bmatrix}E_1^2+H_1^2-\frac{1}{2}(E^2+H^2) & E_1E_2+H_1H_2 & E_3E_1+H_3H_1\\ E_1E_2+H_1H_2 & E_2^2+H_2^2-\frac{1}{2}(E^2+H^2) & E_2E_3+H_2H_3\\ E_3E_1+H_3H_1 & E_2E_3+H_2H_3 & E_3^2+H_3^2-\frac{1}{2}(E^2+H^2)\end{bmatrix} \\ &\sim[\mathrm{J/m^3}]\end{align}

または
\displaystyle T_{ij}=E_iE_j + H_iH_j - \delta_{ij}\frac{1}{2}(E_kE_k+H_kH_k) \tag{1.1}

の固有値\lambda・固有ベクトル\boldsymbol{v}を求めたい．

結果

1個目の固有値・固有ベクトルは *2

\begin{align} \lambda_{(1)} &= -\frac{1}{2}(E^2+H^2) \sim[\mathrm{J/m^3}], \\ \boldsymbol{v}_{(1)}&=\boldsymbol{E}\times\boldsymbol{H} \sim[-]. \end{align} \tag{1.2}

∵Wikipediaによると固有値は
\displaystyle \lambda = -\frac{1}{2}(E^2+H^2 ) , \quad \pm\sqrt{ \left( \frac{E^2 - H^2 }{2} \right)^2 + \left( \boldsymbol{E} \cdot \boldsymbol{H} \right)^2}

らしい．これを信じてみよう．この1個目の固有値は式(1.1)の右辺第3項の係数と同じなので，
\begin{align}0 &= (E_iE_j + H_iH_j )v_j \\ &= (\boldsymbol{E}\cdot\boldsymbol{v})\boldsymbol{E} + (\boldsymbol{H}\cdot\boldsymbol{v})\boldsymbol{H} \end{align}

となるような\boldsymbol{v}が見つかればそれが固有ベクトルになる．それには\boldsymbol vが\boldsymbol{E},\boldsymbol{H}に直交していればよいが，\boldsymbol{E}\times\boldsymbol{H}がそれに適うベクトルだと気づく．

検算しよう．

\begin{align} T_{ij}(\boldsymbol{E}\times\boldsymbol{H})_j &= \left\{E_iE_j + H_iH_j - \delta_{ij}\frac{1}{2}(E^2+H^2)\right\}(\epsilon_{jkl}E_kH_l)\\ &= \epsilon_{jkl}(E_iE_jE_kH_l + H_iH_jE_kH_l) - \frac{1}{2}(E^2+H^2)\epsilon_{ikl}E_kH_l.\end{align}

ここで\epsilon_{jkl}の反対称性より
\begin{align} &= \frac{1}{2}E_i\epsilon_{jkl}(E_jE_k-E_kE_j)H_l + \frac{1}{2}H_i\epsilon_{jkl}(H_jH_l-H_lH_j)E_k \\&\quad- \frac{1}{2}(E^2+H^2)\epsilon_{ikl}E_kH_l\\ &= - \frac{1}{2}(E^2+H^2)\epsilon_{ikl}E_kH_l\\ &= - \frac{1}{2}(E^2+H^2)(\boldsymbol{E}\times\boldsymbol{H})_i. \quad \blacksquare\end{align}

2個目，3個目は

\begin{align} \lambda_{(2)},\lambda_{(3)} &= \pm\sqrt{\left(\frac{H^2-E^2}{2}\right)^2+(\boldsymbol{E}\cdot\boldsymbol{H})^2},\\ \boldsymbol{v}_{(2)} &= (\boldsymbol{E}\cdot\boldsymbol{H}) \boldsymbol{E} + a\boldsymbol{H},\\ \boldsymbol{v}_{(3)} &= (\boldsymbol{E}\cdot\boldsymbol{H}) \boldsymbol{H} - a\boldsymbol{E}, \\ \text{where}\quad a &:= \frac{H^2-E^2}{2} + \sqrt{\left(\frac{H^2-E^2}{2}\right)^2+(\boldsymbol{E}\cdot\boldsymbol{H})^2}. \end{align} \tag{1.3}

∵1個目の固有ベクトルが\boldsymbol{E}\times\boldsymbol{H}なので，他の固有ベクトルはそれに直交，つまり\boldsymbol{E}と\boldsymbol{H}の線形結合で書ける．よって
\boldsymbol{v}=\boldsymbol{E}+a'\boldsymbol{H}

と置いてa'を求めればいい．途中計算は省略するけどT_{ij}をかけると
\begin{align}T_{ij}(E_j+a'H_j) = &\left\{-\frac{H^2-E^2}{2}+a'\boldsymbol{E}\cdot\boldsymbol{H}\right\}E_i \\ &+ \left\{\boldsymbol{E}\cdot\boldsymbol{H}+a'\frac{H^2-E^2}{2}\right\}H_i \end{align}

となって，これが\lambda(E_i+a'H_i)に等しいことから，
\displaystyle \begin{cases} \lambda = -\frac{H^2-E^2}{2} + a'\boldsymbol{E}\cdot\boldsymbol{H},\\ \lambda a' =\boldsymbol{E}\cdot\boldsymbol{H} + a'\frac{H^2-E^2}{2} \end{cases}

となる．これを\lambda,a'について解けば，\lambdaについては式(1.3)のように出て，a'については
\displaystyle a' = \frac{1}{\boldsymbol{E}\cdot\boldsymbol{H}}\left(\frac{H^2-E^2}{2} \pm \sqrt{\left(\frac{H^2-E^2}{2}\right)^2+(\boldsymbol{E}\cdot\boldsymbol{H})^2}\right)

となる．

これで終わってもいいのだが，ちょっと見栄えを良くしておこう．まず，a'のプラスの方を使ってa:=(\boldsymbol{E}\cdot\boldsymbol{H})a'とおくと，2本目の固有ベクトルは

\begin{align} \boldsymbol{v}_{(2)} &= \boldsymbol{E} + \frac{a}{\boldsymbol{E}\cdot\boldsymbol{H}}\boldsymbol{H} \\ &\propto (\boldsymbol{E}\cdot\boldsymbol{H})\boldsymbol{E} + a\boldsymbol{H} \end{align}

と書ける．ここで \propto の変形は，固有ベクトルはその方向だけが大事で大きさはどうでもいいことから行った．
次に，プラスマイナスで2つあるa'はかけると -1 になることに注意する：
\begin{align} & \left\{\frac{1}{\boldsymbol{E}\cdot\boldsymbol{H}}\left(\frac{H^2-E^2}{2} + \sqrt{\left(\frac{H^2-E^2}{2}\right)^2+(\boldsymbol{E}\cdot\boldsymbol{H})^2}\right)\right\} \\ &\cdot \left\{\frac{1}{\boldsymbol{E}\cdot\boldsymbol{H}}\left(\frac{H^2-E^2}{2} - \sqrt{\left(\frac{H^2-E^2}{2}\right)^2+(\boldsymbol{E}\cdot\boldsymbol{H})^2}\right)\right\} \\ &= -1.\end{align}

この関係を利用すると，3本目の固有ベクトルは
\begin{align} \boldsymbol{v}_{(3)} &= \boldsymbol{E} + \left(-\frac{a}{\boldsymbol{E}\cdot\boldsymbol{H}}\right)^{-1}\boldsymbol{H} \\ &\propto (\boldsymbol{E}\cdot\boldsymbol{H}) \boldsymbol{H} - a\boldsymbol{E} \end{align}

と変形できる．■

考察

典型的には，\boldsymbol{v}_{(2)}方向に\lambda_{(2)}>0だから引っ張り力がはたらき，それに垂直な\boldsymbol{v}_{(1)}, \boldsymbol{v}_{(3)}方向に\lambda_{(1)},\lambda_{(3)}<0だから圧縮力がはたらく．
\boldsymbol{E},\boldsymbol{H}が鋭角をなしているとき，\boldsymbol{v}_{(2)}方向は\boldsymbol{E}+\boldsymbol{H}方向に近く，絵で描くとこんな感じか．

E, H, v_{(2)}, v_{(3)}は同一平面上にあり，v_{(1)}はそれらに直交している．

特徴的なケース
  • \boldsymbol{E}\cdot\boldsymbol{H}=0かつE=Hとなる場合（たとえば電磁波），
    1個目は\lambda_{(1)}=-\frac{1}{2}(E^2+H^2),\ \boldsymbol{v}_{(1)} = \boldsymbol{E}\times\boldsymbol{H}のままでいいが，
    2個目3個目については\lambda=0で2重縮退，固有ベクトルは\boldsymbol{E},\boldsymbol{H}の任意の線形結合．
    したがってTは\boldsymbol{E}\times\boldsymbol{H}方向の射影行列となる：
    \displaystyle T_{ij}=-\frac{1}{E^2}(\boldsymbol{E}\times\boldsymbol{H})_i(\boldsymbol{E}\times\boldsymbol{H})_j.
    ∵（対角成分）未証明
    （非対角成分）
    \begin{align} & (\boldsymbol{E}\times\boldsymbol{H})_1(\boldsymbol{E}\times\boldsymbol{H})_2 \\ &= (E_2H_3-E_3H_2)(E_3H_1-E_1H_3) \\ &= E_3H_3(E_1H_2+E_2H_1)-E_1E_2H_3^2-E_3^2H_1H_2. \end{align}
    ここに E_3^2=E^2-E_1^2-E_2^2, H_3^2=E^2-H_1^2-H_2^2, および E_3H_3=-E_1H_1-E_2H_2 を代入することで，
    \begin{align}& (\boldsymbol{E}\times\boldsymbol{H})_1(\boldsymbol{E}\times\boldsymbol{H})_2 \\ &= -(E_1H_1+E_2H_2)(E_1H_2+E_2H_1) \\ & \quad -E_1E_2(E^2-H_1^2-H_2^2)-(E^2-E_1^2-E_2^2)H_1H_2 \\ &= -E^2(E_1E_2+H_1H_2) \\ &= -E^2 T_{12}.\quad\blacksquare\end{align}
  • \boldsymbol{E}\cdot\boldsymbol{H}=0かつE\neq Hとなる場合，
    1個目は変わらず．
    2個目は\lambda_{(2)} = \frac{1}{2}(H^2-E^2),\ \boldsymbol{v}_{(2)} = \boldsymbol{H},
    3個目は\lambda_{(3)}=-\frac{1}{2}(H^2-E^2),\ \boldsymbol{v}_{(3)}=\boldsymbol{E},
  • \boldsymbol{E}と\boldsymbol{H}が平行な場合，
    1個目は\lambda=\frac{1}{2}(E^2+H^2),\ \boldsymbol{v}=\boldsymbol{E},
    2個目3個目は\lambda=-\frac{1}{2}(E^2+H^2),\ \boldsymbol{v}は\boldsymbol{E}に垂直な任意のベクトル．
  • \boldsymbol{H}=0の場合は、*3
    1個目は\lambda=\frac{1}{2}E^2, \boldsymbol{v}=\boldsymbol{E}.
    2個目3個目は \lambda=-\frac{1}{2}E^2, \boldsymbol{v} は \boldsymbol{E} に垂直な任意のベクトル．
    \boldsymbol{E}=0の場合は\boldsymbol{E}と\boldsymbol{H}を入れ替えれば同様．

4次元へ拡張

問題の定式化

4次元の電磁テンソルF_{\mu\nu}を

\begin{align}F_{\mu\nu}&:= \frac{1}{2}\begin{bmatrix}0&E_1&E_2&E_3 \\ -E_1 &0&H_3&-H_2\\ -E_2&-H_3&0&H_1 \\ -E_3&H_2&-H_1&0\end{bmatrix}\\ &=\frac{1}{2}\begin{bmatrix}0 & E_\nu \\ -E_\mu & \epsilon_{\mu\nu\rho}H_\rho\end{bmatrix}\\ & \sim[\mathrm{N^{1/2}/m}] \end{align}

とする．電磁エネルギー運動量テンソル
\displaystyle T_{\mu\nu} = F_{\mu\rho}{F_\nu}^\rho-\frac{1}{4}\eta_{\mu\nu}F_{\rho\sigma}F^{\rho\sigma} \sim[\mathrm{J/m^3}] \tag{2.1}

の固有値\lambda'・固有ベクトルv'_\muを求めたい．

\boldsymbol{E},\boldsymbol{H}を用いると

T_{\mu\nu}=\begin{bmatrix}\frac{1}{2}(E^2+H^2) & \boldsymbol{E}\times\boldsymbol{H} \\ \boldsymbol{E}\times\boldsymbol{H} & -T_{ij}\end{bmatrix} \tag{2.2}

とブロック行列的に表せる（分かりにくいだろうが，T_{\mu\nu}と書いたときは4次元テンソル，T_{ij}と書いたときは3次元テンソルを表す）．3次元の時の結果と無関係だと悲しいので，そのときの結果も参考に使いつつ調べよう．

結果

1, 2個目は式(1.2)が2つに分裂して，*4

\begin{align} \lambda'_{(1)}, \lambda'_{(2)} &= \pm \sqrt{\left(\frac{H^2-E^2}{2}\right)^2 + (\boldsymbol{E}\cdot\boldsymbol{H})^2} \sim[\mathrm{J/m^3}],\\ {v'_\mu}^{(1)} &= \begin{bmatrix}H^2 - a \\ \boldsymbol{E}\times\boldsymbol{H}\end{bmatrix}, \\ {v'_\mu}^{(2)} &= \begin{bmatrix}E^2+a, \\ \boldsymbol{E}\times\boldsymbol{H}\end{bmatrix}. \end{align} \tag{2.3}

3, 4個目は式(1.3)を直接的に拡張したものとなる．固有値は1, 2個目と同じで，
\begin{align} \lambda'_{(3)}, \lambda'_{(4)} &= \pm \sqrt{\left(\frac{H^2-E^2}{2}\right)^2 + (\boldsymbol{E}\cdot\boldsymbol{H})^2},\\ {v'_\mu}^{(3)} &= \begin{bmatrix}0 \\ (\boldsymbol{E}\cdot\boldsymbol{H})\boldsymbol{H} -a\boldsymbol{E} \end{bmatrix},\\ {v'_\mu}^{(4)} &= \begin{bmatrix}0 \\ (\boldsymbol{E}\cdot\boldsymbol{H})\boldsymbol{E} + a\boldsymbol{H} \end{bmatrix}. \end{align} \tag{2.4}

ここでaは式(1.3)と同じく
\displaystyle a := \frac{H^2-E^2}{2} + \sqrt{\left(\frac{H^2-E^2}{2}\right)^2+(\boldsymbol{E}\cdot\boldsymbol{H})^2}.

∵（1個目と2個目について）固有値\lambda'・固有ベクトルv'_\muは
T_{\mu\nu} v'^\nu = \lambda' v'_\mu

を満たすことを再確認しておく．左辺のv'^\nuは反変成分で，右辺のv'_\muは共変成分で書かれていることに注意．

で，まず式(1.2)に対応するものとして

\begin{bmatrix}\frac{1}{2}(E^2+H^2) & \boldsymbol{E}\times\boldsymbol{H} \\ \boldsymbol{E}\times\boldsymbol{H} & -T_{ij}\end{bmatrix} \begin{bmatrix}-v'_0 \\ \boldsymbol{E}\times\boldsymbol{H}\end{bmatrix} = \lambda' \begin{bmatrix}v'_0 \\ \boldsymbol{E}\times\boldsymbol{H}\end{bmatrix}

の形であろうと予想して調べてみる．ここで v'_0 はこれから決めるべきパラメータ．

3次元の時の結果の式(1.2)より

T_{ij}(\boldsymbol{E}\times\boldsymbol{H}) = -\frac{1}{2}(E^2+H^2)\boldsymbol{E}\times\boldsymbol{H}

を利用して左辺を変形すると，
\begin{cases} -\frac{1}{2}(E^2+H^2) v'_0 + |\boldsymbol{E}\times\boldsymbol{H}|^2 = \lambda' v'_0, \\ -v'_0 + \frac{1}{2}(E^2+H^2) = \lambda'\end{cases}

が得られる．これを\lambda', v'_0について解いて，
\begin{align} v'_0 &= \frac{1}{2}\left(E^2+H^2 \pm \sqrt{(E^2+H^2)^2 -4 |\boldsymbol{E}\times\boldsymbol{H}|^2}\right),\\ \lambda' &= \mp \frac{1}{2}\sqrt{(E^2+H^2)^2 -4 |\boldsymbol{E}\times\boldsymbol{H}|^2}. \end{align}

ここで爆速ベクトル計算 *5 を使うとルートの中は
\begin{align}(E^2+H^2)^2 -4 |\boldsymbol{E}\times\boldsymbol{H}|^2 &= (E^2+H^2)^2 -4\left\{E^2H^2-(\boldsymbol{E}\cdot\boldsymbol{H})^2\right\} \\ &= (H^2-E^2)^2 +4(\boldsymbol{E}\cdot\boldsymbol{H})^2 \end{align}

なので固有値・固有ベクトルは上式で表される．■

∵（3個目と4個目について）同様に，式(1.3)の拡張になってると予想してみると，固有ベクトルが\boldsymbol{E}\times\boldsymbol{H}に直交しているのが功を奏して計算が楽になり，最終的に上式が出てくる．
ただしT_{\mu\nu}の中のT_{ij}にはマイナスが付いているので，式(1.3)の\boldsymbol{v}_{(2)}, \boldsymbol{v}_{(3)}に対して{v'_\mu}^{(3)}, {v'_\mu}^{(4)}は入れ替わっているのに注意．■

考察

どんな様子になってるのか，正直全然分からん．

\lambda'_{(1)}=\lambda'_{(3)}>0,\ \lambda'_{(2)}=\lambda'_{(4)}<0になったので，実は2重縮退が2セットあり，4次元時空内に引っ張り力のはたらく平面と，圧縮力のはたらく平面が直交している，という様子になっているようだ．

特徴的なケース

3次元の時の対応物．まだ調べ切れていない．

  • \boldsymbol{E}\cdot\boldsymbol{H}=0かつE=Hとなる場合，上の結果をそのまま計算すると，固有値は4つ全て 0 ，固有ベクトルは
    \begin{align}{v'_\mu}^{(1)} &= {v'_\mu}^{(2)} = \begin{bmatrix} E^2 \\ \boldsymbol{E}\times\boldsymbol{H} \end{bmatrix} = \begin{bmatrix} H^2 \\ \boldsymbol{E}\times\boldsymbol{H} \end{bmatrix}, \\ {v'_\mu}^{(3)} &= {v'_\mu}^{(4)} = 0\end{align}
    となる．実は{v'_\mu}^{(1)}はノルムが 0 のヌルベクトルになっている．
    結局これは，光円錐への射影になってるっぽい．固有値 0 はよく分からんが．*6
    \displaystyle T_{\mu\nu} = \frac{1}{E^2}\begin{bmatrix} E^2 \\ \boldsymbol{E}\times\boldsymbol{H} \end{bmatrix} \begin{bmatrix} E^2 & \boldsymbol{E}\times\boldsymbol{H} \end{bmatrix}.
  • \boldsymbol{E}\cdot\boldsymbol{H}=0かつE\neq Hとなる場合，
    \displaystyle\lambda' = \frac{1}{2}(H^2-E^2) に対し v'_\mu=\begin{bmatrix}E^2 \\ \boldsymbol{E}\times\boldsymbol{H}\end{bmatrix}, \begin{bmatrix}0 \\ \boldsymbol{E}\end{bmatrix},
    \displaystyle\lambda' = -\frac{1}{2}(H^2-E^2) に対し v'_\mu = \begin{bmatrix}H^2 \\ \boldsymbol{E}\times\boldsymbol{H}\end{bmatrix}, \begin{bmatrix}0 \\ \boldsymbol{H} \end{bmatrix}.
  • \boldsymbol{E}と\boldsymbol{H}が平行な場合，
    1個は3次元の時のままで \displaystyle \lambda = \frac{1}{2}(E^2+H^2),\ v^\mu = \begin{bmatrix}0 \\ \boldsymbol{E}\end{bmatrix}.
    あとは3重縮退していて \displaystyle \lambda = -\frac{1}{2}(E^2+H^2),\ v^\mu = \begin{bmatrix}\forall v^t \\ \boldsymbol{E}^\perp\end{bmatrix}.
    ここで\forall v^tは任意の実数，\boldsymbol{E}^\perpは\boldsymbol{E}に3次元の意味で直交する任意のベクトル

その他いろいろ考えたこと

E, Hの入れ替え

3次元の時の式(1.2), (1.3)の固有値・固有ベクトルを\boldsymbol{E},\boldsymbol{H}の関数\lambda(\boldsymbol{E},\boldsymbol{H}), \boldsymbol{v}(\boldsymbol{E},\boldsymbol{H})とみなし，\boldsymbol{E}と\boldsymbol{H}を入れ替える操作を考えてみると，不変になる：

\begin{align} \lambda(\boldsymbol{E},\boldsymbol{H}) \quad &\mapsto \quad \lambda(\boldsymbol{H},\boldsymbol{E}) = \lambda(\boldsymbol{E},\boldsymbol{H}),\\ \boldsymbol{v}(\boldsymbol{E},\boldsymbol{H}) \quad &\mapsto \quad \boldsymbol{v}(\boldsymbol{H},\boldsymbol{E}) = \boldsymbol{v}(\boldsymbol{E},\boldsymbol{H}). \end{align}

∵固有値の方は式(1.2), (1.3)を見れば自明だろう．
固有ベクトルの方は係数
\displaystyle a(\boldsymbol{E},\boldsymbol{H}) = \frac{H^2-E^2}{2} + \sqrt{\left(\frac{H^2-E^2}{2}\right)^2+(\boldsymbol{E}\cdot\boldsymbol{H})^2}
が
\begin{align} a(\boldsymbol{H},\boldsymbol{E}) &= -\frac{H^2-E^2}{2} + \sqrt{\left(\frac{H^2-E^2}{2}\right)^2+(\boldsymbol{E}\cdot\boldsymbol{H})^2} \\ &= \frac{(\boldsymbol{E}\cdot\boldsymbol{H})^2}{a(\boldsymbol{E},\boldsymbol{H})} \end{align}

となるから，
\begin{align} \boldsymbol{v}_{(2)}(\boldsymbol{H},\boldsymbol{E}) &= (\boldsymbol{E}\cdot\boldsymbol{H})\boldsymbol{H} + \frac{(\boldsymbol{E}\cdot\boldsymbol{H})^2}{a(\boldsymbol{E},\boldsymbol{H})}\boldsymbol{E} \\ &\propto (\boldsymbol{E}\cdot\boldsymbol{H})\boldsymbol{E} + a(\boldsymbol{E},\boldsymbol{H})\boldsymbol{H} \\ &= \boldsymbol{v}_{(2)}(\boldsymbol{E},\boldsymbol{H}), \end{align}
\begin{align} \boldsymbol{v}_{(3)}(\boldsymbol{H},\boldsymbol{E}) &= (\boldsymbol{E}\cdot\boldsymbol{H})\boldsymbol{E} - \frac{(\boldsymbol{E}\cdot\boldsymbol{H})^2}{a(\boldsymbol{E},\boldsymbol{H})}\boldsymbol{H} \\ &\propto (\boldsymbol{E}\cdot\boldsymbol{H})\boldsymbol{H} - a(\boldsymbol{E},\boldsymbol{H})\boldsymbol{E} \\ &= \boldsymbol{v}_{(3)}(\boldsymbol{E},\boldsymbol{H}) \end{align}

となりやはり不変であることが分かる．■

まあマクスウェル応力Tが\boldsymbol{E},\boldsymbol{H}について対称だから当たり前ではあるのだが．

これは思い付きだが，逆にTの詳細な構造(1.1)とはあまり関係なく，固有値固有ベクトルが\boldsymbol{E}と\boldsymbol{H}の入れ替えに対して不変，という条件だけで式(1.2), (1.3)は半分くらい導けたりして？　*7

逆問題

派生する問題として，マクスウェル応力Tの固有値\lambda_{(1)}, \lambda_{(2)}, \lambda_{(3)}と固有ベクトルのみが与えられているとき，電場\boldsymbol{E}磁場\boldsymbol{H}はどこまで復元できるだろうか？
と言っても，Tが\boldsymbol{E}と\boldsymbol{H}の入れ替えについて，また\boldsymbol{E}と-\boldsymbol{E}，\boldsymbol{H}と-\boldsymbol{H}の入れ替えについて不変だからそこの違いは無視しないといけない．
また，\lambda_{(1)}<\lambda_{(3)}<0<\lambda_{(2)}=-\lambda_{(3)}とする．

結果，E_2を任意，H_2=\sqrt{-\lambda_{(1)}+\lambda_{(2)}-{E_2}^2} として，

\boldsymbol{E} = \begin{bmatrix}0 \\ E_2 \\ H_2\sqrt{\frac{\lambda_{(1)}+\lambda_{(2)}}{\lambda_{(1)}-\lambda_{(2)}}} \end{bmatrix},\quad \boldsymbol{H} = \begin{bmatrix}0 \\ H_2 \\ -E_2\sqrt{\frac{\lambda_{(1)}+\lambda_{(2)}}{\lambda_{(1)}-\lambda_{(2)}}} \end{bmatrix}

が得られた．

自由度が1個残るとは意外だ．ということは試験電荷とかを用いて電磁的な力が測定できても，電場磁場は一意に定められない．．．ということか．本当か？

前提条件をはずす

最初に言ったように，今回前提として「計算を簡略化するために真空中とし，物理次元を適当に規格化して\epsilon_0=\mu_0=1, \boldsymbol{D}=\boldsymbol{E}, \boldsymbol{B}=\boldsymbol{H}であるかのように扱う」とした．これを外すとどうなるのか？
光速c\sim[\mathrm{m/s}]とインピーダンスZ\sim[\mathrm{Js/C^2}]を復活させ，それぞれの次元を

\begin{align} E_i &\sim[\mathrm{N/C}], & H_i &\sim[\mathrm{A/m}],\\ B_{ij} &= \frac{Z}{c} \epsilon_{ijk}H_k \sim[\mathrm{N/(A\ m)}], & D_{ij} &= \frac{1}{cZ}\epsilon_{ijk}E_k \sim[\mathrm{C/m^2}] \end{align}

と見做し直す．*8

3次元のマクスウェル応力は

\begin{align}T_{ij} &= E_i\epsilon_{jkl}D_{kl} + H_i\epsilon_{jkl}B_{kl} - \delta_{ij}\frac{1}{2}(E_k\epsilon_{klm}D_{lm} + H_k\epsilon_{klm}B_{lm})\\ &\sim[\mathrm{J/m^3}] \end{align}

となる．*9
4次元の方も
\displaystyle F_{\mu\nu} = \begin{bmatrix}0 & E_1 & E_2 & E_3 \\ & 0 & cB_{12} & -cB_{31} \\ &&0& cB_{23} \\ \text{asym.} &&&0 \end{bmatrix} \sim[\mathrm{N/C}],

\begin{align}F^*_{\mu\nu} &= \frac{1}{Z}\epsilon_{\mu\nu\rho\sigma}F^{\rho\sigma}\\ &= \begin{bmatrix}0 & H_1/c & H_2/c & H_3/c \\ & 0 & D_{12} & -D_{31} \\ &&0& D_{23} \\ \text{asym.} &&&0 \end{bmatrix} \sim[\mathrm{C/m^2}] \end{align}

として，
\displaystyle T_{\mu\nu} = \epsilon_{\mu\rho\sigma\lambda}F^{*\sigma\lambda}{F_\nu}^\rho-\frac{1}{4}\eta_{\mu\nu}\epsilon_{\rho\sigma\lambda\kappa}F^{*\lambda\kappa}F^{\rho\sigma}

これをもっと簡略して表したいが，なんかいい方法はないか？

固有値

式(1.3), (2.3), (2.4)の固有値

\displaystyle \lambda^2 = \left(\frac{H^2-E^2}{2}\right)^2+(\boldsymbol{E}\cdot\boldsymbol{H})^2

とは何なんだろうな？　電磁テンソルF_{\mu\nu}を使うと
\lambda^2 = \left(\frac{1}{4}F_{\mu\nu}F^{\mu\nu}\right)^2+\left(\frac{1}{8}\epsilon^{\mu\nu\rho\sigma}F_{\mu\nu}F_{\rho\sigma}\right)^2

となるようだけど，もうちょっと簡単な形にならないものか．
たとえばE, Hの4乗を組み合わせてできるスカラーというところからいくつか考えてみたのだけど，
\begin{align} {F_\alpha}^\beta {F_\beta}^\gamma {F_\gamma}^\delta {F_\delta}^\alpha &= 2(H^2-E^2)^2+4(\boldsymbol{E}\cdot\boldsymbol{H})^2,\\ {F_\alpha}^\beta {F^*_\beta}^\gamma {F_\gamma}^\delta {F^*_\delta}^\alpha &= 4(\boldsymbol{E}\cdot\boldsymbol{H})^2,\\ \epsilon^{\alpha\beta\gamma\delta} \epsilon^{\zeta\eta\theta\iota} F_{\alpha\zeta} F_{\beta\eta} F_{\gamma\theta} F_{\delta\iota} &= 4!\{(E_1^2 H_1^2+E_2^2 H_2^2+E_3^2 H_3^2)\\&\quad +2(E_1H_1E_2H_2+E_2H_2E_3H_3+E_3H_3E_1H_1)\}\end{align}

と，式(2.3),(2.4)の\lambdaと同じでかつ分かりやすいものが思いつかない．

初心に戻って微分形式で

\begin{align} F &=E_i\mathrm{d}t\ \mathrm{d}x^i + B_{ij}\mathrm{d}x^i\ \mathrm{d}x^j,\\ F^*&=H_i\mathrm{d}t\ \mathrm{d}x^i + D_{ij}\mathrm{d}x^i\ \mathrm{d}x^j,\\ \end{align}

とすると，
\begin{align} F\wedge F^* &= (\boldsymbol{E}\cdot\boldsymbol{D+}\boldsymbol{H}\cdot\boldsymbol{B})\mathrm{d}t\ \mathrm{d}x^1\ \mathrm{d}x^2\ \mathrm{d}x^3, \\ F\wedge F &= 2(\boldsymbol{E}\cdot\boldsymbol{B})\mathrm{d}t\ \mathrm{d}x^1\ \mathrm{d}x^2\ \mathrm{d}x^3 \end{align}

となるので
\displaystyle \frac{1}{4}\left\{(F\wedge F^*)^2+(F\wedge F)(F^*\wedge F^*)\right\}

みたいな感じには変形できそうなのだけど．
あ，いかんいかん．この式の各ウェッジ積は4形式になるので，それをさらに2乗とかはできないんだ．言うならば，その4形式の成分だけを取り出さないと．
うーん，分からん．

*1:ランダウリフシッツ抜粋
- p.70: ある系で\boldsymbol{E}\perp \boldsymbol{H},\ E \neq Hなら，ローレンツ変換して\boldsymbol{E}=0または\boldsymbol{H}=0となるような系が見出せる． 逆も言える．
- p.71: H^2-E^2 \propto F_{\mu\nu}F^{\mu\nu}と\boldsymbol{E}\cdot\boldsymbol{H} \propto \epsilon^{\mu\nu\rho\sigma}F_{\mu\nu}F_{\rho\sigma} は不変量である．ここでF_{\mu\nu}は電磁テンソル．
- pp.71-72: 速度をE\times H方向にとってローレンツ変換すれば，EとHが平行になるような系を常に見出せる．（ただし\boldsymbol{E}\perp\boldsymbol{H}かつE=Hである場合を除く）
- pp.92-93: 上2つの変換によって応力テンソルは対角形になる．x軸を場の方向にとればT_{00}=-T_{11}=T_{22}=T_{33}
- p.93: \boldsymbol{E}\perp\boldsymbol{H}かつE=Hである場合，対角化するとx軸をE方向に，y軸をH方向にとるとT_{00}=T_{30}=T_{33}のみが非ゼロ．

*2:固有ベクトルは適当にスケーリングしてもよいので，暗黙の内に正規化されているとみなし，次元も無次元とする．

*3:Wikipediaには\boldsymbol{E}のみの場合，固有値・固有ベクトルは

\displaystyle \lambda = - \frac{ E^2 }{2} ,~ -\frac{ E^2 }{2} ,~ +\frac{ E^2 }{2}

\boldsymbol{v} = \boldsymbol{E} \times \boldsymbol{E}_y ,~ -\boldsymbol{E} \times \boldsymbol{E}_z ,~ \boldsymbol{E} E_x

とか書いてあるが，この固有ベクトルの書き方はいただけない．要はE方向が1つ，それに直角な方向が2つ（縮退）と言いたいだけなのに，余計な情報がくっついている．

*4:4次元と3次元それぞれの固有値の関係は，{\lambda'_{(1)}}^2 = \lambda_{(1)}^2 - |\boldsymbol{E}\times\boldsymbol{H}|^2.

*5:備忘：爆速ベクトル計算 - wetchのブログ

*6:ランダウリフシッツp.306には固有値のうち一組は0になるとか書いてあるが，どう関係するのか？

*7:たとえば，p,q,rを\boldsymbol{E},\boldsymbol{H}に依存する未知係数として，

\begin{align} \boldsymbol{v}_{(2)}(\boldsymbol{E},\boldsymbol{H}) &= (\boldsymbol{E}\cdot\boldsymbol{H})\boldsymbol{E} + p\boldsymbol{H},\\ \boldsymbol{v}_{(3)}(\boldsymbol{E},\boldsymbol{H}) &= q\boldsymbol{E} + r\boldsymbol{H},\\ \boldsymbol{v}_{(2)}(\boldsymbol{H},\boldsymbol{E}) &= \boldsymbol{v}_{(2)}(\boldsymbol{E},\boldsymbol{H}),\\ \boldsymbol{v}_{(3)}(\boldsymbol{H},\boldsymbol{E}) &= \boldsymbol{v}_{(3)}(\boldsymbol{E},\boldsymbol{H}),\\ \boldsymbol{v}_{(2)}(\boldsymbol{E},\boldsymbol{H}) \cdot \boldsymbol{v}_{(3)}(\boldsymbol{E},\boldsymbol{H}) &= 0 \end{align}
という条件からp,q,rを求めれば式(1.3)が大体出そうな気がする．

*8:Zはただのスカラー定数ではなく，必ずレビチビタ\epsilon_{ijk}とセットで現れ，擬量の空間と非擬量の空間を渡るためのものなのだと思う．

*9:本来\epsilon_{ijk}\epsilon_{ljk}=2\delta_{il}だから係数2の帳尻を合わせなければならないが，省略．

電流と磁場，電磁誘導のイラスト

電磁気学

電磁場を説明するイラスト，というか落書きをもう少し考えてみた．

アンペールの法則

直線電流

Qクーロンの点電荷は電束を“Q”に比例するだけの“本”数，略して“Q本”伴っている，みたいな考え方はガウスの法則の説明としてよく知られている．

https://detail-infomation.com/wp-content/uploads/2020/05/電束とは-600x221.jpg*1

それに類似するように，Iアンペアの直線電流は磁場の面を伴っていて，その枚数はIに比例する枚数，略してI枚であると考える．
すると電流の周りを一周する閉曲線Cが貫く磁場の面の枚数も当然I枚である．これがアンペールの法則

\displaystyle \oint_\mathrm{C} H \cdot \mathrm{d}l = I
のイメージ．

たとえば閉曲線Cが電流を中心とする半径rの円周であるなら，C上で磁場は一定でCの長さが2\pi rということだから，磁場の面の線密度，すなわち磁場は

\displaystyle H=\frac{I}{2\pi r} \tag{1}
となる．
上の図を正面から見たところ．破線は閉曲線Cを表す．

蛇足だが，この磁場の面は磁位の等値面とは考えない．

円形電流

電流Iが半径rの円形電流の場合，それに伴う磁場は実際は無限遠方まで存在し，こんな感じになる：


だけど、簡略化して次の図のように考えてしまおう：
円形電流の断面図．rは円の半径．
電流が伴うj枚の磁場の面は半径と同じrの距離までしか届かない．すると円の中心での磁場の強さが
\displaystyle H=\frac{I}{2r} \tag{2}

となることがイメージできるだろう．

「直線電流の式(1)には\piが付いて，円電流の式(2)には付かないので間違えないように覚えましょう」*2なんてこと言わないでも，この絵で理解するほうがわかりやすいと思う．

コイル

コイルの中の磁場はこんな感じになる：

コイルの断面図．茶色がコイルに流れる電流，橙色が磁場の面

  • 磁場の面はコイルの外部には出ない
  • 1本の電流は磁場の面をI枚伴う
  • その電流が1mあたりn巻きにされている

ということから

H=nI

がイメージできる．

電磁誘導

磁束線のループを1本考える（磁石か電磁石でもあったとする）．
磁石を動かすと磁束線の残像として電場が生じる．

磁束（茶色）のループが画面奥から手前への向きに動いているとき，電場（青）は磁束の残像として生じる．向きはレンツ則より決まる．
生じた電場がたまたま導線を横切れば，その導線の内部に電場が生じるわけだから電流が流れる．

*1:https://detail-infomation.com/electric-flux/

*2:たとえば直線電流、円形電流の作る磁場の公式 - どっちにπが入るか混ざるので... - Yahoo!知恵袋

偏微分の順序交換可能性って見た目で判別できないのか？

物理学・数学

2変数関数f(x,y)の偏微分の順序交換可能性，つまり

\displaystyle f_{xy} \equiv \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right) = f_{yx} \equiv \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right)

とできるのはいつか？を考える．

別サイト*1を確認すると，3つの十分条件があって，前提条件の強い順に書くと

  • fがC^2級（全ての2階の偏導関数が存在して連続）ならよし．
  • f_{xy}とf_{yx}が存在していずれも連続ならよし．f_{xx}, f_{yy}の存在は仮定しない．
  • ​(SchwarzまたはClairaut) f_x, f_y, f_{xy}が存在して，f_{xy}が連続ならよし．f_{yx}の存在は後からついてくる．

というのがあるらしい．

たとえば

f(x,y) = \begin{cases} \dfrac{xy(x^2 - y^2)}{x^2+y^2} & \mbox{ for } (x, y) \ne (0, 0)\\ 0 & \mbox{ for } (x, y) = (0, 0) \end{cases}

が原点で順序交換不可能ということだが．．．
これってグラフの見た目では判別できないのか？
googleに書かせてみたグラフがこんな感じなんだが．

普通に滑らかな関数にしか見えない．
だとしたら今まで、「まあ多分交換可能だろ」と思って外微分を2回かけたらゼロにしてたけど，意外とそうとは言えない場合も多いかもしれない気がしてきて心配になってきた．

いや，物理ではこういうのをあまりうるさく言わない流儀なのは分かってはいるんだけど．

*1:偏微分の順序交換の十分条件とその証明 | 高校数学の美しい物語,
ヤングの定理 - Wikipedia