共分散と相関係数
１、共分散
2次元確率変数(X,Y)の共分散の定義：Cov(X,Y)=E{[X-E(X)][Y-E(Y)]}
E(X)：Xの期待値、E(Y)：Ｙの期待値
共分散Cov(X,Y)は、確率変数間の関係を表す特徴指標。それは、Ｘの標準偏差【X-E(X)】とＹの標準偏差【Y-E(Y)】の的乗積の期待値からなる。
共分散Cov(X,Y)>0の場合，XとY正の相関关
共分散Cov(X,Y)<0の場合，XとY負の相関关
共分散Cov(X,Y)=0の場合，XとY無相関关
例(正の相関)：
2次元確率変数（身長X，体重Y）
|
|
身高X（cm） |
体重Y（500g） |
X-E(X) |
Y-E(Y) |
[X-E(X)][Y-E(Y)] |
|
1 |
152 |
92 |
-19.4 |
-39.7 |
770.18 |
|
2 |
185 |
162 |
13.6 |
30.3 |
412.08 |
|
3 |
169 |
125 |
-2.4 |
-6.7 |
16.08 |
|
4 |
172 |
118 |
0.6 |
-13.7 |
-8.22 |
|
5 |
174 |
122 |
2.6 |
-9.7 |
-25.22 |
|
6 |
168 |
135 |
-3.4 |
3.3 |
-11.22 |
|
7 |
180 |
168 |
8.6 |
36.3 |
312.18 |
|
|
E(X) =171.4 |
E(Y) =131.7 |
|
|
E{[X-E(X)][Y-E(Y)]}=209.4 |
共分散Cov(X,Y)＝209.4、直観と同じ、身長と体重は正の相関になる。
例(負の相関)：
2次元確率変数（遊びの時間X，学校の成績Y）
|
|
遊び時間X（h/日） |
学校の成績Y |
X-E(X) |
Y-E(Y) |
[X-E(X)][Y-E(Y)] |
|
1 |
0 |
95 |
-1.36 |
20.7 |
-28.152 |
|
2 |
1 |
65 |
-0.36 |
-9.3 |
3.348 |
|
3 |
3 |
70 |
1.64 |
-4.3 |
-7.052 |
|
4 |
2 |
55 |
0.64 |
-19.3 |
-12.352 |
|
5 |
2.5 |
65 |
1.14 |
-9.3 |
-10.602 |
|
6 |
0.5 |
80 |
-0.86 |
5.7 |
-4.902 |
|
7 |
0.5 |
90 |
-0.86 |
15.7 |
-13.502 |
|
|
E(X) =1.36 |
E(Y) =74.3 |
|
|
E{[X-E(X)][Y-E(Y)]}= -10.5 |
共分散Cov(X,Y)＝-10.5、直観と同じ、遊びの時間と成績は負の相関になる。
２、相関係数
共分散は「相関」という関係がわかるが、どれぐらい相関しているかはわからない。
上の例の209.4や-10.5という数値が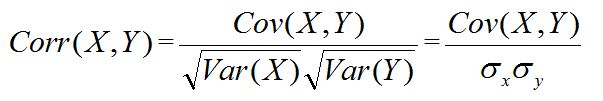
出ているが、結局何を意味しているかはわからない。そのため、相関係数の出番になるあ。
定義：
Corr(X,Y)=1の場合：完全の正の相関。即ち：Y=aX+b，a>0
Corr(X,Y)=-1の場合：完全の負の相関。即ち：Y=-aX+b，a>0
0 < |Corr(X,Y)| < 1の場合：ある程度線形相関。
Corr(X,Y)=0の場合：線形関係なし。※無関係ではない。
先の２つの例
身長体重：Corr(X,Y)= 209.4/(10.2*24.4)=0.84
遊び時間と成績：Corr(X,Y)= -10.5/(1.1*13.4)= -0.71
